Базовые предпосылки модели
В модели рассматривается закрытая экономика. Фирмы максимизируют свою прибыль. Фирмы функционируют в условиях совершенной конкуренции. Производится только один продукт Y{displaystyle Y}, используемый, как для потребленияC{displaystyle C}, так и для инвестицийI{displaystyle I}. Темпы технологического прогрессаg{displaystyle g}, роста населения n{displaystyle n} и норма выбытия капитала δ{displaystyle delta } — постоянны и задаются экзогенно. Норма сбереженийs{displaystyle s} также задаётся экзогенно[7]. Фискальная политика (государственные расходы и налоги) в модели отсутствует. Время t{displaystyle t} изменяется непрерывно[3][2].
Предпосылка о закрытой экономике означает, что произведенный продукт тратится на инвестиции и потребление, экспорт/импорт отсутствуют, сбережения равны инвестициям: S=I=sY{displaystyle S=I=sY}, Y=C I{displaystyle Y=C I}[8].
Производственная функцияY(K,L,E){displaystyle Y(K,L,E)} удовлетворяет неоклассическим предпосылкам[9][10]:
1) технологический прогресс увеличивает производительность труда (нейтрален по Харроду): Yt=Y(Kt,LtEt), Et=E0egt, g=const{displaystyle Y_{t}=Y(K_{t},L_{t}E_{t}), E_{t}=E_{0}e^{gt}, g=const};
2) в производственной функции используются трудL{displaystyle L} и капиталK{displaystyle K}, она обладает постоянной отдачей от масштаба: Y(aK,aLE)=aY(K,LE){displaystyle Y(aK,aLE)=aY(K,LE)};
3) предельная производительность факторов положительная и убывающая: ∂Y∂K>0, ∂2Y∂K2<0, ∂Y∂L>0, ∂2Y∂L2<0{displaystyle {frac {partial Y}{partial K}}>0, {frac {partial ^{2}Y}{partial K^{2}}}<0, {frac {partial Y}{partial L}}>0, {frac {partial ^{2}Y}{partial L^{2}}}<0};
4) производственная функция удовлетворяет условиям Инады, а именно, если запас одного из факторов бесконечно мал, то его предельная производительность бесконечно велика, если же запас одного из факторов бесконечно велик, то его предельная производительность бесконечно мала: limK→0∂Y∂K=limL→0∂Y∂L= ∞, limK→ ∞∂Y∂K=limL→ ∞∂Y∂L=0{displaystyle lim _{Kto 0}{frac {partial Y}{partial K}}=lim _{Lto 0}{frac {partial Y}{partial L}}= infty , lim _{Kto infty }{frac {partial Y}{partial K}}=lim _{Lto infty }{frac {partial Y}{partial L}}=0};
5) для производства необходим каждый фактор: Y(K,0)=Y(0,LE)=0{displaystyle Y(K,0)=Y(0,LE)=0}.
Население Lt{displaystyle L_{t}}, равное в модели совокупным трудовым ресурсам, растет с постоянным темпом n{displaystyle n}[3]: Lt=L0ent, n=const{displaystyle L_{t}=L_{0}e^{nt}, n=const}.
Для поиска решения модели используются удельные показатели[8]: выпуск на единицу эффективного труда y=YLE{displaystyle y={frac {Y}{LE}}}, запас капитала на единицу эффективного труда k=KLE{displaystyle k={frac {K}{LE}}}, потребление на единицу эффективного труда c=CLE{displaystyle c={frac {C}{LE}}}, инвестиции на единицу эффективного труда i=ILE{displaystyle i={frac {I}{LE}}}.
Тогда производственную функцию можно записать в следующем виде: y=YLE=Y(KLE,1)=f(k){displaystyle y={frac {Y}{LE}}=Y{biggl (}{frac {K}{LE}},1{biggr )}=f(k)}.
Наиболее часто в качестве конкретного примера производственной функции, удовлетворяющей предпосылкам модели, используется производственная функция Кобба-Дугласа[9][11]:
- Y(K,LE)=Kα(LE)1−α, y=kα, 0<α<1{displaystyle Y(K,LE)=K^{alpha }(LE)^{1-alpha }, y=k^{alpha }, 0<alpha <1},
где α{displaystyle alpha } — эластичность выпуска по капиталу, (1−α){displaystyle (1-alpha )} — эластичность выпуска по труду.
Поведение потребителей в явном виде в модели не рассматривается. Функция полезности отсутствует. Вместо этого имеется экзогенно задаваемая норма сбережений s{displaystyle s}, 0<s<1{displaystyle 0<s<1}, означающая, что домохозяйства сберегают долю своего дохода s{displaystyle s}, а оставшуюся долю 1−s{displaystyle 1-s} тратят на потребление, и это соотношение не зависит от происходящих в экономике событий[12].
Модель экономического роста солоу
После работ А. Смита, Д. Рикардо, Т. Мальтуса сформировалась классическая модель экономического роста, которая под давлением критики сменилась неоклассической моделью, чья последующая критика приводит в 1986-1988 годах к формированию эндогенных моделей (П. Ромер, Р. Лукас, С. Ребело и др.) долгосрочный экономический рост формируется уже внутри модели, модели стали эндогенными.
Неоклассические модели роста преодолевали ряд ограничений кейнсианских моделей (Е. Домара, Р. Харрода и др.), позволив более точно описать особенности макроэкономических процессов.
Модель Солоу (Солоу – Свана) – неоклассическая модель, основанная на производственной функции с замещением факторов производства с учетом экзогенного нейтрального технического прогресса, труда и капитала как факторов экономического роста.
Р. Солоу показал, что нестабильность динамического равновесия в кейнсианских моделях была следствием невзаимозаменяемости факторов производства. Вместо функции Леонтьева с жестко фиксированными пропорциями использования факторов производства Y = min{aX1, bX2} он использовал в своей модели производственную функцию Кобба-Дугласа Y = F(K, L), в которой труд L и капитал K являются субститутами (заменителями). Другими предпосылками анализа в модели Солоу являются: убывающая предельная производительность капитала, постоянная отдача от масштаба, постоянная норма выбытия, отсутствие инвестиционных лагов.
Взаимозаменяемость факторов (изменение капиталовооруженности) объясняется не только технологическими условиями, но и неоклассической предпосылкой о совершенной конкуренции на рынках факторов.
Необходимым условием равновесия экономической системы является равенство совокупного спроса и предложения. Предложение описывается производственной функцией с постоянной отдачей от масштаба 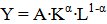 , и для любого положительного z верно: zF(K, L) = F(zK, zL). Тогда если z = 1/L, то Y/L = F(K/L). Получаем производственную функцию удельного выпуска на одного работника.
, и для любого положительного z верно: zF(K, L) = F(zK, zL). Тогда если z = 1/L, то Y/L = F(K/L). Получаем производственную функцию удельного выпуска на одного работника.
Обозначим Y/L через у, а К/L через k и перепишем исходную функцию в форме взаимосвязи между производительностью и фондовооруженностью (капиталовооруженностью) работника: у = f(k) (рис. 2.16).
|
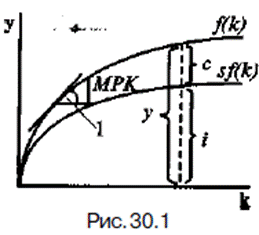
Тангенс угла наклона данной производственной функции соответствует предельному продукту капитала (МРК), который убывает по мере роста фондовооруженности (k).
Совокупный спрос в модели Солоу определяется инвестициями и потреблением:
y = i c, (2.36)
где i и с – инвестиции и потребление в расчете на одного занятого.
Доход делится между потреблением и сбережениями в соответствии с нормой сбережения, так что потребление можно представить как
c = (l – s)∙y, (2.37)
где s – норма сбережения (накопления).
Тогда у = с i = (1 – s)∙y i, откуда i = s∙y. В условиях равновесия инвестиции равны сбережениям и пропорциональны доходу.
Условия равенства спроса и предложения могут быть представлены как
f(k) = c i или f(k) = (1 – s)∙y i. (2.38)
Производственная функция определяет предложение на рынке товаров, а накопление капитала – спрос на произведенный продукт.
Динамика объема выпуска зависит от объема капитала (в нашем случае – капитала в расчете на одного занятого, или капиталовооруженности). Объем капитала меняется под воздействием инвестиций и выбытия: инвестиции увеличивают запас капитала, выбытие – уменьшает.
Инвестиции зависят от фондовооруженности и нормы накопления, что следует из условия равенства спроса и предложения в экономике: i = s∙f(k). Норма накопления определяет деление продукта на инвестиции и потребление при любом значении k (см. рис. 2.16): y = f(k) => i = s∙f(k), c = (1 – s)∙f(k).
Амортизационные отчисления учитываются следующим образом: если принять, что ежегодно вследствие износа капитала выбывает его фиксированная часть d (норма выбытия), то величина выбытия будет пропорциональна объему капитала и равна d∙k. На графике эта связь отражается прямой, выходящей из точки начала координат, с угловым коэффициентом d (рис. 2.17).
|

Влияние инвестиций и выбытия на динамику запасов капитала можно представить уравнением
∆k = i – d∙k, (2.39)
или, используя равенство инвестиций и сбережений, ∆k = s∙f(k) – d∙k.
Запас капитала (k) будет увеличиваться (∆k > 0) до уровня, при котором инвестиции будут равны величине выбытия, т.е. s∙f(k) = d∙k. После этого запас капитала на одного занятого (фондовооруженность) не будет меняться во времени, поскольку две действующие на него силы уравновесят друг друга (∆k = 0).
Уровень запаса капитала, при котором инвестиции равны выбытию, называется равновесным (устойчивым) уровнем фондовооруженности труда и обозначается k*. При достижении k* экономика находится в состоянии долгосрочного равновесия.
Равновесие является устойчивым, поскольку независимо от исходного значения k экономика будет стремиться к равновесному состоянию k*. Если начальное k1 ниже k*, то валовые инвестиции будут больше выбытия (s∙f(k) > d∙k) и запас капитала будет возрастать на величину чистых инвестиций. Если k2 > k*, это означает, что инвестиции меньше, чем износ, а значит запас капитала будет сокращаться, приближаясь к уровню k* (см. рис. 2.17).
Норма накопления (сбережения) непосредственно влияет на устойчивый уровень фондовооруженности. Рост нормы сбережения с s1 до s2 сдвигает кривую инвестиций вверх из положения s1∙f(k) до s2∙(k) (рис. 2.18).
В исходном состоянии экономика имела устойчивый запас капитала k1*, при котором инвестиции равнялись выбытию. После повышения нормы сбережения инвестиции выросли на (i’1 – i1), а запас капитала (k1*) и выбытие (d∙k) остались прежними. В этих условиях инвестиции начинают превышать выбытие, что вызывает рост запаса капитала до уровня нового равновесия k2*, которое характеризуется более высокими значениями фондовооруженности и производительности труда (выпуск на одного занятого y).
|
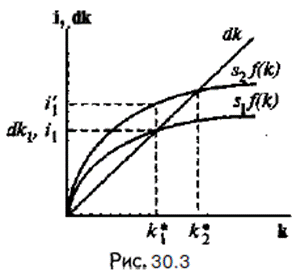
Таким образом, чем выше норма сбережения (накопления), тем более высокий уровень выпуска и запаса капитала может быть достигнут в состоянии устойчивого равновесия. Однако повышение нормы накопления ведет к ускорению экономического роста в краткосрочном периоде, до тех пор, пока экономика не достигнет точки нового устойчивого равновесия.
Очевидно, что ни сам процесс накопления, ни увеличение нормы сбережения не могут объяснить механизм непрерывного экономического роста. Они показывают лишь переход от одного состояния равновесия к другому.
Для дальнейшего развития модели Солоу поочередно снимаются две предпосылки моделирования, отраженного на рис. 2.16-2.18, – неизменность численности населения и его занятой части (их динамика предполагается одинаковой) и отсутствие технического прогресса. Вначале модель описывает, как система приходит в равновесие при отсутствии учета технического прогресса (т.е. при нейтральности технического прогресса) и постоянной отдаче от масштаба, затем в нее вводятся технологические сдвиги посредством изменения нормы накопления капитала и убывающей отдачи от масштаба.
Пусть население растет с постоянным темпом n. Это фактор, влияющий вместе с инвестициями и выбытием на фондовооруженность. Теперь уравнение, показывающее изменение запаса капитала на одного работника (2.39), будет выглядеть как:
∆k = i – d∙k – n∙k = i – (d n)∙k. (2.40)
Рост населения, как и выбытие, снижает фондовооруженность, хотя и по-другому – не через уменьшение наличного запаса капитала, а путем распределения его между возросшим числом занятых. В данных условиях необходим такой объем инвестиций, который не только бы покрыл выбытие капитала, но и позволил бы обеспечить капиталом новых рабочих в прежнем объеме. Произведение n∙k показывает, сколько требуется дополнительного капитала в расчете на одного занятого, чтобы капиталовооруженность новых рабочих была на том же уровне, что и прежних.
Условие устойчивого равновесия в экономике при неизменной фондовооруженности k* можно будет записать теперь так:
∆k = s∙f(k) – (d n) k = 0 или s∙f(k) = (d n)∙k. (2.41)
Данное состояние характеризуется полной занятостью ресурсов труда и капитала (рис. 2.19).
|


В устойчивом состоянии экономики капитал и выпуск на одного занятого, т.е. фондовооруженность (k) и производительность труда (у) остаются неизменными. Но чтобы фондовооруженность оставалась постоянной и при росте населения, капитал должен возрастать с тем же темпом, что и население, т.е.:
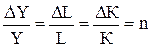
Таким образом, рост населения становится одной из причин непрерывного экономического роста в условиях равновесия.
Отметим, что с увеличением темпа роста населения возрастает угловой коэффициент кривой (d n)∙k, что приводит к уменьшению равновесного уровня фондовооруженности (k*), а следовательно, к падению у.
Учет в модели Солоу технологического прогресса видоизменяет исходную производственную функцию, так как предполагается трудосберегающая форма технологического прогресса. Производственная функция будет иметь вид Y = F(К, L∙E), где Е – эффективность труда, a (L∙E) – численность условных единиц труда с постоянной эффективностью Е. Чем выше Е, тем больше продукции может быть произведено данным числом работников. Предполагается, что технологический прогресс осуществляется путем роста эффективности труда Е с постоянным темпом g. Рост эффективности труда в данном случае аналогичен по результатам росту численности занятых: если технологический прогресс имеет темп g = 2 %, то, например, 100 рабочих могут произвести столько же продукции, сколько ранее производили 102 рабочих. Если теперь численность занятых (L) растет с темпом n, а эффективность труда растет с темпом g, то (L∙E) будет увеличиваться с темпом (n g).
Включение технологического прогресса несколько меняет и анализ состояния устойчивого равновесия, хотя ход рассуждений сохраняется. Если определить k как количество капитала в расчете на единицу труда с постоянной эффективностью, то результаты роста эффективных единиц труда, аналогичны росту численности занятых (увеличение количества единиц труда с постоянной эффективностью снижает величину капитала, приходящегося на одну такую единицу). В состоянии устойчивого равновесия (см. рис. 2.19) уровень фондовооруженности k* уравновешивает, с одной стороны, влияние инвестиций, повышающих фондовооруженность, а с другой стороны, воздействие выбытия, роста числа занятых и технологического прогресса, снижающих уровень капитала в расчете на эффективную единицу труда:
s∙∆k = (d n g)∙k. (2.43)
В устойчивом состоянии (k*) при наличии технологического прогресса общий объем капитала (К) и выпуска (Y) будут расти с темпом (n g). Но в отличие от случая роста населения, теперь будут расти с темпом g фондовооруженность K/L и выпуск Y/L в расчете на одного занятого; последнее может служить основой для повышения благосостояния населения. Технологический прогресс в модели Солоу является, следовательно, единственным условием непрерывного роста уровня жизни, поскольку лишь при его наличии наблюдается устойчивый рост выпуска на душу населения (у).
Таким образом, в модели Солоу найдено объяснение механизма непрерывного экономического роста в режиме равновесия при полной занятости ресурсов.
Как известно, в кейнсианских моделях (Р. Харрод, Е. Домар) норма сбережения задавалось экзогенно и определяла величину равновесного темпа роста дохода. В неоклассической модели Солоу при любой норме сбережения рыночная экономика стремится к соответствующему устойчивому уровню фондовооруженности (k*) и сбалансированному росту, когда доход и капитал растут с темпом (n g). Величина нормы сбережения (накопления) является объектом экономической политики и важна при оценке различных программ экономического роста.
Поскольку равновесный экономический рост совместим с различными нормами сбережения (увеличение s лишь на короткое время ускоряло рост экономики, в длительном же периоде экономика возвращалась к устойчивому равновесию и постоянному темпу роста в зависимости от значения n и g), возникает проблема выбора оптимальной нормы сбережения.
Оптимальная норма накопления, соответствующая «золотому правилу» Э. Фелпса, обеспечивает равновесный экономический рост с максимальным уровнем потребления. Устойчивый уровень фондовооруженности, соответствующий этой норме накопления, обозначим k**, а потребления – с**.
Уровень потребления в расчете на одного занятого при любом устойчивом значении фондовооруженности определяется путем ряда преобразований исходного тождества: у = с i. Выражаем потребление с через у и i и подставляем значения данных параметров, которые они принимают в устойчивом состоянии:
c = y – i, с* = f(k*) – d∙k*, (2.44)
где с* – потребление в состоянии устойчивого роста.
По определению устойчивого уровня фондовооруженности i = s∙f(k) = d∙k. Теперь из различных устойчивых уровней фондовооруженности (k*), соответствующих разным значениям s, необходимо выбрать такой, при котором потребление достигает максимума (рис. 2.20).
|
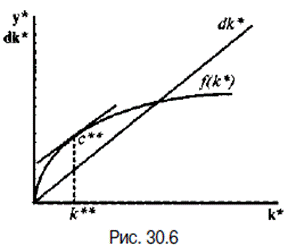
Если выбрано k* < k**, то объем выпуска увеличивается в большей степени, чем величина выбытия (линия f(k*) на графике круче, чем d∙k*), а значит, разница между ними, равная потреблению, растет. При k* > k** увеличение объема выпуска меньше роста выбытия, т.е. потребление падает. Рост потребления возможен лишь до точки k**, где оно достигает максимума (производственная функция и кривая d∙k* имеют здесь одинаковый наклон). В этой точке увеличение запаса капитала на единицу даст прирост выпуска, равный предельному продукту капитала (МРК), и увеличит выбытие на величину d (износ на единицу капитала). Роста потребления не будет, если весь прирост выпуска будет использован на увеличение инвестиций для покрытия выбытия капитала. Таким образом, при уровне фондовооруженности, соответствующем «золотому правилу» (k**), должно выполняться условие: МРК = d (предельный продукт капитала равен норме выбытия), а с учетом роста населения и технологического прогресса: МРК = d n g.
Если экономика в исходном состоянии имеет запас капитала, больший, чем следует по «золотому правилу», необходима программа по снижению нормы накопления. Эта программа обусловливает увеличение потребления и снижение инвестиций. При этом экономика выходит из состояния равновесия и вновь достигает его при пропорциях, соответствующих «золотому правилу».
Если экономика в исходном состоянии имеет запас капитала меньше, чем k**, необходима программа, направленная на повышение нормы сбережения. Эта программа первоначально приводит к росту инвестиций и падению потребления, но по мере накопления капитала с определенного момента потребление вновь начинает расти. В результате экономика достигает нового равновесия, но уже в соответствии с «золотым правилом», где потребление превышает исходный уровень.
Данная программа обычно считается непопулярной в связи с наличием «переходного периода», характеризующегося падением потребления, поэтому ее принятие зависит от межвременных предпочтений политиков, их ориентации на краткосрочный или долгосрочный результат.
Рассмотренная модель Солоу позволяет описать механизм долгосрочного экономического роста, сохраняющий равновесие и полную занятость факторов производства. Она выделяет технический прогресс как единственную основу устойчивого роста благосостояния и позволяет найти оптимальный вариант роста, обеспечивающий максимум потребления.
Представленная модель не свободна и от недостатков. Модель анализирует состояния устойчивого равновесия, достигаемые в долгосрочной перспективе, тогда как для экономической политики важна и краткосрочная динамика производства и уровня жизни. Многие экзогенные переменные модели Солоу (s, δ, n, g) было бы предпочтительнее определять внутри модели, поскольку они тесно связаны с другими ее параметрами и могут видоизменять конечный результат. Так, в модели существует возможность динамической неэффективности, т. е. возможность избыточного накопления капитала по сравнению с уровнем «золотого правила»; этот результат является следствием экзогенного задания нормы сбережения. Также модель не включает также целый ряд ограничителей роста, существенных в современных условиях, – ресурсных, экологических, социальных. Используемая в модели функция Кобба-Дугласа, описывая лишь определенный тип взаимодействия факторов производства, не всегда отражает реальную ситуацию в экономике. Эти и другие недостатки пытаются преодолеть современные теории экономического роста.
Современные теории эндогенного роста пытаются определить устойчивый темп роста в самой модели (т.е. эндогенно), связывая его со всеми возможными количественными и качественными факторами: ресурсными, институциональными.
§
Недостатки модели Солоу (в силу экзогенности задания ряда ключевых параметров экономического роста, таких как норма сбережений и темп роста НТП) привели к разработке моделей эндогенного роста. Сомнения в модели Солоу возникли при объяснении темпа роста в послевоенной Японии при высокой ставке процента по сравнению с США при низкой ставке процента.
Самый простой вариант получения постоянного роста экономики – введение в модель производственной функции, имеющей постоянную отдачу от факторов производства, – линейной производственной функции. В этом случае исключается предположение об убывании предельной производительности, которое является основным условием достижения неоклассической моделью устойчивого состояния. Самой простой среди моделей эндогенного роста является АК-модель Р. Лукаса.
АК-модель экономического роста Р. Лукаса – эндогенная модель роста, в которой производственная функция линейно зависит от объема капитала К и имеет форму Y = A∙K (А – постоянный параметр производительности, A > 0), а выпуск на одного работника y зависит от капиталовооружённости k: y = A∙k, k = K/L. В ней делается попытка объяснить экономический рост, не привлекая предпосылку об экзогенно задаваемых темпах роста НТП.
Составными частями ее стали:
1) условие оптимальности и межвременная функция полезности домохозяйств Ф. Рамсея (1928);
2) производственная функция типа АК Д. Неймана (1937);
3) капитал, который рассматривается Ф. Найтом (1944) как совокупность физического и человеческого капитала;
4) эндогенная ставка сбережения Д. Касса (1965) и Т. Купманса (1963).
Предположение о зависимости объема выпуска экономики только от объема капитала здесь объясняется широким пониманием капитала, в который включается и собственно физический капитал, и человеческий капитал, знания, общественная инфраструктура и т.д. Если убывание предельной производительности возникает вследствие снижения отдачи от добавочной единицы одного фактора, при постоянстве других, при таком понимании отсутствие убывания объясняется с возрастанием всех факторов одновременно, в том числе и знаний (технического прогресса), которое делает возможным новую технологическую комбинацию большего объема факторов.
Как и в неоклассической модели Солоу, предполагается динамическое равновесие валовых инвестиций и сбережений, которое имеет вид дифференциального уравнения:
∆k = s∙y – (d n)∙k = s∙A∙k – (d n)∙k, (2.45)
где s – норма сбережений;
d – норма амортизации (выбытия);
n – темп прироста населения (занятых).
Отсюда темп прироста капиталовооруженности в устойчивом состоянии (аналогично неоклассической модели) равен, при условии постоянства параметров модели, постоянной величине:
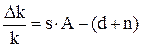
Это означает, что постоянный темп прироста капиталовооруженности в устойчивом состоянии равен темпу прироста национального продукта на душу населения и темпу прироста подушевого потребления:
 . (2.47)
. (2.47)
Этот темп зависит от поведения параметров модели, например, более высокая норма сбережений s приведет к повышению долгосрочных темпов роста. Это же произойдет и в случае улучшения технологии А. Изменение нормы амортизации и темпа роста населения также имеют постоянный эффект на темп роста γ.
В итоге модели доказывается, что чем дальше страна отстоит от устойчивого уровня, тем выше ее темп экономического роста.
В целом, АК-модель преодолевает недостаток неоклассических моделей в части экзогенности устойчивого роста, зависимости от внешних факторов, не зависящих от поведения экономических агентов. Устойчивый постоянный экономический рост в АК-модели зависит от поведенческих и институциональных параметров (таких как норма сбережения и пропорциональная налоговая ставка), что достигается благодаря исключению убывающей предельной отдачи капитала. В данной модели экономический рост зависит от установленной государством ставки подоходного налогообложения, т.е. от государственного регулирования экономики.
§
Модель Р. Лукаса представляет два аспекта объяснения человеческого капитала. С одной стороны, рассматривается общий уровень умений (профессионализма) (general skill level), воплощаемый в производительности лиц, занятых в производстве. Этот уровень (h) колеблется в интервале 0 < h < 1. Производственный ресурс (N) – это не просто число людей, занятых в производстве, а люди с учетом присущего им уровня умений: N = N(h). С другой стороны, речь идет о запасе человеческого капитала. Модель учитывает то, что в каждом обществе формируется определенный средний запас человеческого капитала (hа), на его накопление направлена часть времени кроме того, которое посвящено собственно производственной деятельности. Накопление человеческого капитала рассматривается как проявление социальной активности.
С первым аспектом трактовки человеческого капитала – уровнем профессионализма занятых – связывается его внутренний эффект. Он воплощается в большей производительности и большем доходе собственника этого ресурса. Со вторым аспектом – формированием определенного, среднего для общества, запаса человеческого капитала связывается внешний эффект – выгода для всех субъектов экономики. Предусматривается, что факт существования общей выгоды от запаса человеческого капитала не принимается во внимание отдельными субъектами при распределении времени на занятость собственно производительной деятельностью (u) и накопление человеческого капитала (1 – u).
Указанные положения о человеческом капитале воплощаются в динамической производственной функции вида
Y(t) = N(t)∙c(t) K(t) = A∙K(t)β∙[u(t)∙h(t)∙N(t)]1-β∙ha(t)y, (2.48)
где N(t)∙c(t) – сумма расходов на потребление домохозяйств;
K(t) – сумма расходов на прирост капитала;
А – постоянная величина, отражающая уровень технологий;
K(t) – запас физического капитала;
[u(t)∙h(t)∙N(t)] – показатель эффективной рабочей силы;
ha(t)r – внешний эффект от запаса человеческого капитала для общества;
t – период времени.
Производственная функция (2.48) отражает оба аспекта человеческого капитала. То, что он есть проявление определенного уровня умений (профессионализма), представлено корректировкой количества занятых N(t) на уровень умений h(t) и на долю времени, уделенного собственно производственной деятельности u(t). То, что запас человеческого капитала имеет позитивный внешний эффект, который увеличивает общий выпуск, отражено множителем hα(t)y.
Производственная функция (2.48) предусматривает возрастающую отдачу ресурсов, поскольку β (1 – β) γ > 1. Факт роста отдачи связан именно с появлением позитивных внешних эффектов от запаса человеческого капитала.
Модель П. Ромера основана на разграничении структурных элементов человеческого капитала. Это структурирование дает возможность избавиться от двузначности. Основной смысл структурирования – отражение различного влияния составляющих человеческого капитала на продукт (выпуск). Такими составляющими являются:
L – физические способности лиц, занятых в производстве;
Е – образование по результатам обучения в начальной и средней школе;
Z – совокупный опыт, приобретенный в процессе работы;
S – научные знания (опыт), полученные после средней школы.
Есть принципиальное отличие между L, Е, Z, с одной стороны, и S – с другой. Здесь допускается, что научные знания S вносят непосредственный вклад в создание предметов потребления. Поэтому производственная функция в части создания предметов потребления имеет следующий вид:
C = C(LC,EC,ZC,XC), (2.49)
где С – производство предметов потребления;
XС – промежуточный продукт, используемый в производстве конечной продукции.
Хотя в уравнении (2.49) отсутствуют переменные, отражающие научные знания (S), а также физический капитал (К), они присутствуют там опосредованно – через переменную X. Объяснение механизма этого опосредованного влияния побуждает к дальнейшей детализации понятия «научные знания»: в модели различаются прикладная и фундаментальная наука. Именно прикладная наука обеспечивает развитие сектора исследований и разработок (R&D) и материализуется в продуктах. В частности, под влиянием прикладной науки происходит увеличение перечня товаров промежуточного производства (X). С учетом именно такого влияния прикладных знаний и происходит модификация производственной функции. В привычном (как функция Кобба – Дугласа) виде она такова:
G(L,E,Z,X) = Lα∙Eβ∙Zγ∙ 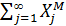 . (2.50)
. (2.50)
Причем предусматривается тождество производственных функций для потребительских (С) и капитальных (промежуточного потребления Xj) товаров. Следовательно, выполняется условие: G(L,E,Z,X) = Xj(L, E,Z,X) = C(L, E, Z, X).
Последнее иллюстрирует влиятельность прикладных научных знаний для всей экономики.
В этой модели речь идет о неизменной отдаче ресурсов, то есть о возможности устойчивого экономического роста, поскольку α β γ μ = 1.
Особого внимания заслуживает такое уточнение П. Ромера о роли образования: экономический прогресс обеспечивается не приростом показателя образования (Е), а его достигнутым уровнем. Этот вывод сделан на основе регрессионного анализа. Выяснено, что существует тесная связь между показателем уровня грамотности населения и инвестициями. А уже инвестиции (и накопление физического капитала) существенно воздействуют на темп экономического роста. Эту логическую цепочку можно представить следующим образом: Е → I → К → у.
§
Модель Г. Мэнкью – Д. Ромера – Д. Уэйла –экзогенная модель экономического роста при убывающей отдаче физического и человеческого капитала и экзогенном темпе прироста технологии.
Имеет три принципиальные особенности. Во-первых, введение в модель такой категории, как человеческий капитал, подчинено цели усовершенствования модели Солоу, которая объясняет экономический рост через механизм сбережения и прирост населения. Параметр человеческого капитала оказался той переменной, которая обеспечила лучшие результаты регрессионного анализа на основе межстрановых сравнений.
Во-вторых, человеческий капитал ограничивается средним школьным образованием, а его уровень оценивается через прямые расходы правительства. Авторы осознают недостатки такой оценки, связанные с неучетом косвенных расходов в виде недополученных во время учебы заработных плат и расходов семей на образование. Вторая потенциальная составляющая – медицина – не включена в анализ, как подчеркивают авторы, ввиду технических сложностей. По поводу науки как возможной составляющей человеческого капитала указано, что развитие научных знаний отражается переменной g (темпом технического прогресса, по модели Солоу). Допускается, что переменная g не имеет существенных различий между странами, и потому в анализе она принимается как постоянная величина. Таким путем научные знания фактически выведены за пределы собственно человеческого капитала.
Поскольку человеческий капитал ограничен средним образованием, постольку используется особый прием оценки уровня накопления человеческого капитала – через процент населения трудоспособного возраста, учащегося в школе.
В-третьих, внимание концентрируется на общих, а не отличительных чертах человеческого и физического капитала, а именно:
— предусматривается одинаковая норма замещения для обоих видов капитала, что отражается в допущении о трансформации единицы потребления в единицу или физического, или человеческого капитала;
— принимается одинаковая норма износа для физического (σк) и человеческого (σн) капитала.
Человеческий капитал введен в производственную функцию как отдельный ресурс наряду с физическим капиталом следующим образом:
Y(t) = K(t)а∙Н(t)β∙(A(t)∙L(t))1-а-β, (2.50)
где H(t) – человеческий капитал.
В рассматриваемой модели принято, что α β ≤ 1, следовательно, речь идет то убывающей отдаче производственных ресурсов. При фиксированном значении α может иметь место большое число значений β. Поэтому имеется в виду возможность различных вкладов человеческого капитала в создание продукта при обеспечении устойчивого состояния экономики у*, значение которого выводится подобно тому, как это сделано в модели Солоу; оно имеет следующий вид:
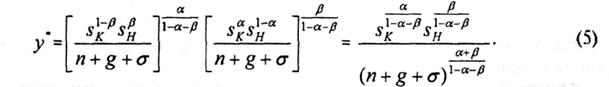
Различив склонность к сбережению по физическому (Sк – доля дохода, инвестируемая в физический капитал) и человеческому капиталу (Sн – доля дохода, инвестируемая в человеческий капитал) и воспользовавшись логикой модели Солоу, приведем уравнение накопления для обоих видов капитала:
∆k = sK∙y – (n g a)∙k – уравнение накопления физического капитала;
∆h = sH∙y – (n g a)∙h – уравнение накопления человеческого капитала,
где y = Y/(A∙L), k = K/(A∙L), h = H/(A∙L), y = ka∙hβ.
Частным случаем модели Мэнкью – Ромера – Уэйла является модель Д. Ромера – эндогенная модель экономического роста при постоянной отдаче человеческого и физического капитала и отсутствии технического прогресса. Она также включает человеческий капитал в объяснение роста через расширение модели Солоу. Поэтому допускается, что факторами роста наряду с техническим прогрессом, склонностью к сбережениям и темпом прироста населения является направление части ресурсов на накопление человеческого капитала. К тому же четко разграничиваются абстрактное и конкретное знание: при объяснении человеческого капитала принимается во внимание только конкретное, изменяющее производительность знание.
Модель Д. Ромера предусматривает такие определяющие черты человеческого капитала:
— он проявляется в приобретенной профессиональной способности, навыках и конкретных знаниях работников;
— накопление каждым работником человеческого капитала (усвоение им новых знаний и навыков) растет на базе уже приобретенного запаса;
— есть две его стороны – неквалифицированный труд (raw labor), как бы полученный работником по наследству, и производственные навыки, знания, приобретенные специально;
— он может быть оценен через количество лет обучения.
Два последних положения определяют способ представления величины человеческого капитала:
H(t) = L(t)∙G(E), (2.52)
где L(t) – общее количество работников, используемое для измерения обычного (неквалифицированного) труда;
G(E) – функция квалифицированного труда, зависимая от количества лет обучения среднего работника;
Е – среднее количество лет обучения одного работника.
В основу модели положена производственная функция вида
Y(t) = K(t)α∙[A(t)∙H(t)]l-a, (2.53)
где A(t) – коэффициент эффективности труда;
H(t) – человеческий капитал, или общий объем производственных услуг квалифицированных работников.
Исходя из производственной функции (2.53) выпуск на единицу эффективного труда, учитывающего человеческий капитал, определяется следующим образом:
y = Y/(A∙G(E)∙L) = Y/(A∙H). (2.54)
Тогда выпуск на одного работника будет определяться так:
Y/L = A∙G(E)∙y, (2.55)
где A∙G(E) – количество единиц эффективного труда на одного работника;
у – выпуск на единицу эффективного труда.
Оценка человеческого капитала через годы учебы предусматривает расширение модели Солоу в еще одном направлении. Речь идет об учете различия, для упрощения проигнорированного в модели Солоу, а именно между работающими и всем населением страны. Поскольку человеческий капитал связан с годами учебы, то его накопление предусматривает изменение соотношения между количеством обучающегося населения и работающего в пользу первого. Доля работающих L в общем количестве населения N определяется по формуле:
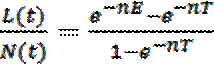 , (2.55)
, (2.55)
где Т – годы жизни;
Е – годы учебы;
(Т – Е) – годы работы;
n – темп изменения количества населения.
С учетом доли работающих в населении страны можно определить выпуск на одного работника:
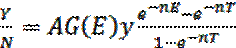 . (2.56)
. (2.56)
Из уравнения (2.56) следует, что увеличение лет учебы, приходящихся на среднего работника, имеет как положительное (благодаря росту G(E)), так и отрицательное (из-за уменьшения доли работающих в структуре населения 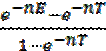 ) воздействие. Поэтому в модели закономерно может быть поставлен вопрос о выводе «золотого правила» (по аналогии с «золотым правилом» в модели Солоу) касательно лет учебы, по которому оптимизируется темп экономического роста продукта на одного работника. Вклад человеческого капитала в рост здесь определяется путем логарифмирования и декомпозиции уравнения производственной функции Y(t) = K(t)α∙[A(t)∙H(t)]l—a. В результате получается выражение
) воздействие. Поэтому в модели закономерно может быть поставлен вопрос о выводе «золотого правила» (по аналогии с «золотым правилом» в модели Солоу) касательно лет учебы, по которому оптимизируется темп экономического роста продукта на одного работника. Вклад человеческого капитала в рост здесь определяется путем логарифмирования и декомпозиции уравнения производственной функции Y(t) = K(t)α∙[A(t)∙H(t)]l—a. В результате получается выражение
ln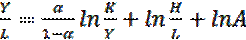 . (2.57)
. (2.57)
Оценивая результаты эмпирической проверки модели экономического роста по логике уравнения (2.57), Д. Ромер концентрирует внимание на двух ее недостатках:
1) неучете возможных экстерналий, связанных с человеческим капиталом, следовательно, трактовке различий между странами по показателю Y/L, которые вызваны изменениями параметра А, в то время как они могли быть связаны с изменениями в человеческом капитале;
2) игнорировании в случае оценки человеческого капитала исключительно через годы учебы тех различий между странами, которые связаны с качеством сферы образования, неформальным (вне учебных заведений) накоплением знаний, обучением в процессе работы, уровнем воспитания детей и пр.
Таким образом, по результатам анализа четырех моделей имеется несколько вариантов ответов на сформулированные вопросы об участии человеческого капитала в экономическом росте.
A. Уровень человеческого капитала может оцениваться:
— по производительности (доходу) лиц, занятых в производстве;
— по расходам правительства на образование;
— по количеству лет учебы лиц, принимающих участие в продуктивной деятельности.
Б. Накопление человеческого капитала может проявляться через:
— изменение доли времени, затраченного вне собственно производственной деятельности в пользу обучения;
— процент населения трудоспособного возраста, занятого учебой в школе;
— изменение соотношения между теми, кто работает, и теми, кто учится.
B. В качестве составляющих (структурных элементов) человеческого капитала могут анализироваться:
— физические способности, образование, опыт, конкретные знания;
— образование, физическое состояние работающих, связанное с медицинским обслуживанием, развитие знаний, непосредственно влияющих на темп технического прогресса.
Г. Воздействие ресурса «человеческий капитал» на продукт (выпуск) может представляться как:
— непосредственное (при рассмотрении его в качестве отдельного ресурса наряду с материальным капиталом и трудом, при возникновении положительных внешних эффектов от его накопления, при учете особого вклада каждого отдельного элемента человеческого капитала в создание продукта);
— опосредованное (через воздействие на интегральный показатель эффективной рабочей силы, через изменение структуры капитальных благ (товаров промежуточного потребления), которые первыми реагируют на развитие прикладной науки в секторе R&D);
— положительное (благодаря изменению производительности труда занятых в производстве);
— отрицательное (в силу отвлечения от производственной деятельности лиц, занятых учебой).
Понятно, что важность рассмотренных моделей экономического роста с участием человеческого капитала определяется возможностью практического применения идей, в них представленных.
2.18 Модель экономического роста Рамсея (Рамсея – Касса – Купманса)
Модель Ф. Рамсея – Д. Касса – Т. Купманса или модель Рамсея – модель эндогенного экономического роста, в которой «траектория» потребления и сбережений определяются на основе решения задачи оптимизации домашних хозяйств и фирм в условиях совершенной конкуренции.
Ее составными частями стали:
1) условие оптимальности и межвременная функция полезности домохозяйств Ф. Рамсея (1928);
2) метод оптимального потребления в неоклассической модели роста на основе эндогенной ставки сбережения Д. Касса (1965) и Т. Купмпанса (1963).
В модели используется репрезентативное домашнее хозяйство с динамикой его потребительского и сберегательного поведения. Предполагается закрытая экономика с реальными переменными (в единицах товаров и услуг) в условиях совершенной конкуренции. Условно предполагается, что решения этого домохозяйства эквивалентны решениям бесконечно живущего индивида, который учитывает текущее и будущее благосостояние и ресурсы. Задача потребительского выбора или функция полезности этого индивида, представляющего все население, имеет вид:
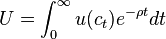 ,
,
где 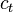 – потребление на душу населения в момент времени
– потребление на душу населения в момент времени 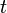 .
.
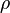 – положительный коэффициент дисконтирования, отражающий межвременные предпочтения индивида.
– положительный коэффициент дисконтирования, отражающий межвременные предпочтения индивида.
Функция полезности 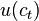 является сепарабельной, то есть зависит только от потребления в этот момент. Кроме этого, предполагается что предельная полезность – производная u'(c) – является положительной и убывающей функцией и при стремлении потребления к нулю, предельная полезность стремится к бесконечности, а при стремлении потребления к бесконечности предельная полезность стремится к нулю.
является сепарабельной, то есть зависит только от потребления в этот момент. Кроме этого, предполагается что предельная полезность – производная u'(c) – является положительной и убывающей функцией и при стремлении потребления к нулю, предельная полезность стремится к бесконечности, а при стремлении потребления к бесконечности предельная полезность стремится к нулю.
Доходы «индивида» складываются из заработной платы  и доходов
и доходов  от активов
от активов  , принадлежащих ему и имеющих доходность
, принадлежащих ему и имеющих доходность 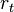 (активы могут быть также и отрицательными, что отражает ситуацию чистого долга, причем ставка по заемным средствам предполагается одинаковой с доходностью положительных активов). При этом доходы тратятся либо на потребление, либо на увеличение активов (сбережения). Таким образом, увеличение активов в единицу времени равно
(активы могут быть также и отрицательными, что отражает ситуацию чистого долга, причем ставка по заемным средствам предполагается одинаковой с доходностью положительных активов). При этом доходы тратятся либо на потребление, либо на увеличение активов (сбережения). Таким образом, увеличение активов в единицу времени равно 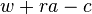 . Необходимо также учесть, что население растет темпом
. Необходимо также учесть, что население растет темпом 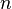 , поэтому активы на одного человека сокращаются с этим же темпом, то есть скорость изменения активов в каждый момент времени уменьшаются на
, поэтому активы на одного человека сокращаются с этим же темпом, то есть скорость изменения активов в каждый момент времени уменьшаются на 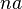 . Таким образом, окончательно бюджетное ограничение индивида имеет вид
. Таким образом, окончательно бюджетное ограничение индивида имеет вид
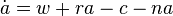 .
.
Задача оптимизации поведения потребителя заключается в максимизации 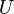 при данном ограничении. Cтроится функция Гамильтона:
при данном ограничении. Cтроится функция Гамильтона:
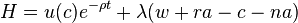
и условия максимума
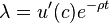 и
и 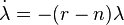 .
.
Отсюда выводится уравнение динамики потребления:
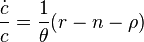 ,
,
где 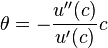 – эластичность предельной полезности по потреблению.
– эластичность предельной полезности по потреблению.
Эта эластичность является положительной в силу положительности предельной полезности и отрицательности второй производной полезности (убывающая предельная полезность).
Для существования стационарного состояния необходимо, чтобы 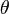 асимптотически стремилась к постоянной величине, поэтому в качестве функции полезности
асимптотически стремилась к постоянной величине, поэтому в качестве функции полезности 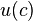 используют функцию следующего вида:
используют функцию следующего вида:
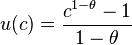 ,
,
где 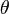 – постоянная эластичность предельной полезности по потреблению.
– постоянная эластичность предельной полезности по потреблению.
Помимо задачи потребителя в модели также решается и задача фирмы. Рассматривается репрезентативная фирма, производственная функция которой описывает совокупное предложение. Производственная функция является неоклассической и аналогичной производственной функции в модели Солоу: 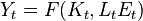 , где
, где 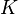 – капитал,
– капитал, 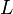 – труд,
– труд, 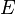 – эффективность труда. Предполагается, что эффективность труда растет с постоянным темпом
– эффективность труда. Предполагается, что эффективность труда растет с постоянным темпом 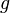 .
.
В силу однородности функции можно записать 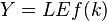 , где
, где 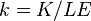 – капиталовооруженность труда с постоянной эффективностью. Тогда
– капиталовооруженность труда с постоянной эффективностью. Тогда
 – предельная производительность труда,
– предельная производительность труда,
 – предельная производительность труда, где в целях упрощения, предполагается, что эффективность труда в нулевой момент времени равна единице, поэтому динамика эффективности труда описывается как
– предельная производительность труда, где в целях упрощения, предполагается, что эффективность труда в нулевой момент времени равна единице, поэтому динамика эффективности труда описывается как 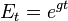 .
.
В условиях совершенной конкуренции предельные производительности по факторам производства равны ценам этих факторов. Цена трудовых ресурсов равна заработной плате 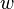 , а цена капитала равна
, а цена капитала равна 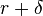 , где
, где 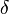 – темп износа капитала. Тогда
– темп износа капитала. Тогда
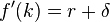
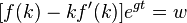
Поскольку рассматривается закрытая экономика, то капитал принадлежит резидентам и удельный капитал на одного работника (K/L) равен активам 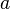 .
.
По аналогии с моделью Солоу можно записать уравнение динамики капиталовооруженности труда с постоянной эффективностью:
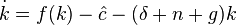
где 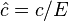 – потребление на единицу труда с постоянной эффективностью.
– потребление на единицу труда с постоянной эффективностью.
Учитывая, что 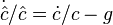 , исходя из решения задачи потребителя можно записать следующее уравнение
, исходя из решения задачи потребителя можно записать следующее уравнение
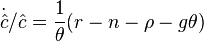
или с учетом равенства 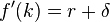 в задаче фирмы:
в задаче фирмы:
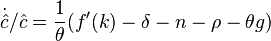
Данное дифференциальное уравнение вместе с дифференциальным уравнением для капиталовооруженности 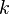 и определяют экономическую динамику в рамках данной модели.
и определяют экономическую динамику в рамках данной модели.
В модели Солоу устанавливалось «золотое правило» сбережений, максимизирующее потребление. В модели Рамсея это правило модифицируется и имеет вид:
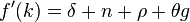 ,
,
что соответствует постоянному потреблению на единицу труда с постоянной эффективностью (или рост потребления на одного человека с темпом 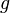 ).
).
Модель объясняет основные макроэкономические закономерности, однако не объясняет причин мирового экономического роста. Общий долгосрочный рост в этой модели обеспечивает параметр эффективности труда, который не объясняется в модели, а задаётся экзогенно.
В модели Рамсея динамическая неэффективность отсутствует, поскольку выбор нормы сбережения является результатом оптимального решения экономических агентов.
§
Модель пересекающихся поколений (модель П. Самуэльсона – П. Даймонда)– модель экзогенного экономического роста в условиях совершенной конкуренции, отличительной особенностью которой является дискретность времени и взаимосвязь экономических показателей с результатами предыдущего периода.
Составные части модели:
1) на основе причин процентного дохода на капитал П. Самуэльсон (1958) предложил модель экономики с двумя типами индивидов – молодые и старые. Молодые работают и получают доход от труда, старые не работают, они тратят свои сбережения. Модель предназначалась для анализа, сколько сбережений делается в экономике, как сбережения превращаются в инвестиции;
2) объединение П. Даймондом (1965) модели Самуэльсона и модели экономического роста Солоу с учетом дополнений модели Рамсея.
В модели делается ряд допущений:
— время изменяется дискретно (скачкообразно);
— экономика закрытого типа (без внешнего рынка);
— производится только одно благо, которое может как потребляться, так и инвестироваться;
— факторы производства – труд и капитал;
— производственная функция с постоянной отдачей от масштаба, 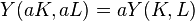 ;
;
— нейтральный (по Харроду) технический прогресс с темпом  :
: 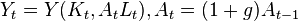 ;
;
— совершенная конкуренция: факторы производства оплачиваются по их предельным продуктам;
— в период 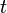 рождается
рождается 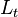 индивидов;
индивидов;
— постоянный темп прироста населения 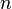 , то есть
, то есть 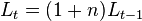 ;
;
— каждый индивид живёт только два периода (молодость и старость);
— в начале весь капитал 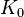 находится у пожилых, на начало других периодов капитал равен сбережениям молодого поколения
находится у пожилых, на начало других периодов капитал равен сбережениям молодого поколения 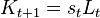 ;
;
— молодой индивид предлагает единицу труда (предложение труда неэластично) и получает натуральную заработную плату (в единицах товара);
— норма выбытия капитала задается экзогенно и является постоянной, лаг капитальных вложений отсутствует.
В период 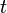 живёт
живёт 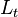 молодых и
молодых и 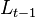 пожилых индивидов. В молодости индивид рождается и работает. Получаемое за труд вознаграждение распределяется на текущее потребление и сбережения. В старости индивид не получает новых доходов, тратит накопленные сбережения и умирает. Альтруистические связи между поколениями отсутствуют: к концу жизни пожилые полностью расходуют свои накопления, молодые не наследуют ничего, но и не помогают старикам.
пожилых индивидов. В молодости индивид рождается и работает. Получаемое за труд вознаграждение распределяется на текущее потребление и сбережения. В старости индивид не получает новых доходов, тратит накопленные сбережения и умирает. Альтруистические связи между поколениями отсутствуют: к концу жизни пожилые полностью расходуют свои накопления, молодые не наследуют ничего, но и не помогают старикам.
Считается, что индивид стремится увеличить суммарное потребление в первом и во втором периоде жизни (целевая функция), но имеет ограниченный ресурс в виде размера оплаты за свой труд.
Расчеты в модели показали, что потребление превышает уровень «золотого правила» Солоу, оставалось бы выше устойчивого уровня. Это означает, что экономика является динамически неэффективной, а рыночное равновесие не является оптимальным по Парето. Вывод представляется неожиданным, поскольку устойчивое равновесие – результат оптимального решения экономических агентов. Возможность неоптимальности по Парето получается из-за того, что в модели принимают решение индивиды, живущие конечный отрезок времени, тогда как время жизни экономики в целом не ограничено. Если индивиды в рыночной экономике хотят потреблять в старости, они должны сберегать в молодости, даже если ставки процента малы. Управляющий орган в централизованной экономике может перераспределять при таких обстоятельствах ресурсы от молодых к старым. Чтобы не ухудшить при этом положение молодых, он может снова перераспределять ресурсы в их пользу в следующем периоде, когда они станут старыми, и т. д. Если устойчивый уровень капиталовооруженности остается выше уровня «золотого правила», такой способ перераспределения ресурсов оказывается эффективнее накопления.
§
Экономические субъекты принимают динамические решения в ситуации неопределенности будущего. Поэтому при оценке поведения экономических субъектов в динамических моделях макроэкономики определяющее значение имеет учет их ожиданий – в отношении уровня доходов, цен, безработицы. Развитие научных представлений об ожиданиях в экономике привело к разработке трех основных концепций, рассматривающих принципы формирования ожиданий и описывающих эти принципы в различных макроэкономических моделях – концепции экстраполяционных (статистических), адаптивных и рациональных ожиданий.
Концепция экстраполяционных (статистических) ожиданий базируется на гипотезе о том, что экономические субъекты при формировании своих ожиданий учитывают тенденции, которые сложились в прошлом, и распространяют ихна будущее (средний уровень цен, процентная ставка, уровень инфляции и т.д.). Концепция адаптивных ожиданий предполагает, что в экономике субъекты формируют свои ожидания с учетом прошлых ошибок или с учетом очевидных или обозначившихся изменений макроситуации. Сторонники концепции рациональных ожиданий считают, что рассмотренные выше модели слишком упрощенно представляют процесс формирования экономическими субъектами будущих оценок. Они считают, что люди используют иные способы оценок, особенно в тех случаях, когда речь идет о распределении значительных денежных средств. Рационально действующие субъекты не только учитывают ошибки прошлого, но и заглядывают в будущее. Они строят свое поведение на основе сбора и анализа всей совокупности информации об изменениях экономики в будущем. Гипотеза сама по себе не определяет, какими конкретно должны быть ожидания экономических субъектов. Конкретизация моделей формирования ожиданий предполагает необходимость учета связей прогнозируемого показателя с определяющими его переменными. Поэтому для разных показателей могут использоваться разные модели.
Так, согласно концепции статистических ожиданий, существует определенная, четко формализуемая альтернатива между инфляцией и безработицей, поэтому кривая Филлипса интерпретируется на уровне догмы. Рост совокупного спроса в условиях статистических ожиданий будет сопровождаться и повышением спроса на факторы производства; в результате безработица упадет ниже естественного уровня до значения u1, при этом инфляция возрастет с π0 до π1 (рис. 2.21).

Рисунок 2.21 – Кривая Филипса для статистических ожиданий
Государство стимулирует совокупный спрос AD↑, тем самым повышает уровень занятости и сокращает безработицу; плата за сокращение безработицы с u1 до u0 – повышение уровня инфляции с π0 до π1; отказ от стимулирующей политики возвращает AD1 в положение AD0 (рис. 2.21, а). Это возможно благодаря статичности ожиданий экономических субъектов, которые не меняют своих планов в части продажи факторов производства; кривая AS статична.
Так как субъекты статичны в своих ожиданиях, то цены на факторы не растут; издержки производства снижаются; спрос на труд растет. Отказ от стимулирующей политики возвращает экономическую систему в первоначальное положение. Сдвиг кривой Филлипса вправо-вверх (Ph0 → Ph1) возможен только в случае шока предложения.
Теория адаптивных ожиданий – концепция макроэкономики, описывающая процесс образования ожиданий у экономических агентов о развитии экономических величин. В отличие от теории рациональных ожиданий адаптивные ожидания образуются только на основе наблюдений развития этих величин в прошлом. Например, факт систематической недооценки уровня инфляции в прошлом, влияет на оценку инфляции в будущем.
Пример: {displaystyle pi _{-1}^{e}}πе-1 – ожидаемый уровень инфляции в этом году, а{displaystyle pi _{-1}} π-1 – действительный уровень инфляции. По теории адаптивных ожиданий ожидаемый уровень инфляции следующего года равен:
πе = πе-1 λ∙(π-1 – πе-1), (2.70)
где λ – число между 0 и 1.
Ожидаемая инфляция следующего года соответствует сумме из ожидаемой инфляции в этом году и коррекции ошибки. Коррекция ошибки соответствует разнице между ожидаемой и действительной инфляцией одного года, однако может учитывать ошибки любого количества лет.
В соответствии с концепцией адаптивных ожиданий экономические субъекты корректируют свои ожидания с учетом ошибок прошлых лет. Тем не менее, на краткосрочных временных отрезках кривая Филлипса достаточно ясно выражена. Во-первых, субъекты реагируют на изменения экономической конъюнктуры с некоторым запозданием, так как не имеют полной и достоверной информации. Во-вторых, при условии, что уровень инфляции растет, ожидания субъектов будут постоянно отставать от его фактических значений.
Разовые мероприятия в рамках стимулирующей политики могут привести к росту занятости и национального дохода. Графически это можно интерпретировать как перемещение вдоль кривой Филлипса Ph1 при смещении кривой AD вправо: AD0 в положение AD1. В результате безработица уменьшится с u* до u1 (рис. 2.22).

Рисунок 2.22 – Кривая Филипса при адаптивных ожиданиях
В отличие от случая статистических ожиданий экономические субъекты на изменения в совокупном спросе реагируют с некоторым опозданием. При этом в определенной степени идет адаптация к изменениям конъюнктуры и действиям Правительства. Для достижения более высокого уровня занятости u1 → u* необходимо не только поддержание более высокого уровня инфляции, но и его ускорение. Каждому уровню инфляции соответствует своя кривая Филипса.
Однако после того как экономические субъекты адаптируются к изменениям конъюнктуры, они начнут пересматривать условия продажи факторов производства, что вызовет сдвиг кривой совокупного предложения вверх. Восстановление предложения будет сопровождаться смещением кривой Филлипса вправо-вверх. В результате занятость возвратится к своему первоначальному значению, но при более высоком уровне инфляции (рис. 2.22, б).
Теория рациональных ожиданий – макроэкономическая концепция, разработанная Дж. Мутом (1961) и Р. Лукасом (середина 70-х гг. ХХ в). Была разработана как противопоставление теории адаптивных ожиданий. Основная идея заключается в том, что экономические агенты используют всю доступную информацию и не совершают систематической ошибки в своих прогнозах (ожиданиях), в отличие от модели адаптивных ожиданий, в которой ожидания лишь постепенно (асимптотически) адаптируются к изменениям.
Теория рациональных ожиданий исходит из следующих фундаментальных положений.
1. Экономика должна постоянно функционировать на основе рыночного саморегулирования.
2. Хозяйственные агенты гибко реагируют на изменение конъюнктуры, действуя в соответствии с принципами оптимизации, ориентируясь на реальные экономические результаты.
3. Кризисы являются результатом ошибок экономических субъектов в течение краткосрочного периода.
Основоположник теории Джон Мут исходил из того, что экономические агенты располагают всей доступной для них информацией и используют ее в целях прогноза хозяйственного процесса в такой модели экономики, какую они себе представляют и считают правильной, действуя при этом рационально, хотя и субъективно. Это подразумевает, что участники рынка знакомы с механизмами рынка и в состоянии прогнозировать реакцию спроса и предложения в результате изменения цен.
Р. Лукасом была разработана модель несовершенной информации, одним из наиболее значительных следствий из которой является функция совокупного предложения Лукаса. Далее, модель Мута и Лукаса, описанная выше, исходит из того, что на экономическом рынке существует лишь один вариант равновесия и образование ожиданий происходит именно вокруг него. Лукас предполагал, что это равновесие достигается при полной занятости.
Согласно модели, выпуск в экономике является функцией цен, не согласующихся с рациональными ожиданиями. Функцию предложения Ys в соответствии с теорией рациональных ожиданий можно представить в следующем виде:
YS = f(P – Pe), (2.72)
где Pe – ожидаемая цена.
Теория рациональных ожиданий была разработана как противопоставление теории адаптивных ожиданий, в которой образование ожиданий основывается исключительно на наблюдении показателей прошлого, а не всей доступной информации, как это предполагает теория рациональных ожиданий. Равновесие в теории адаптивных ожиданий достигается лишь асимптотически.
В соответствии с концепцией рациональных ожиданий экономические субъекты адекватно реагируют на изменения экономической конъюнктуры, так как обладают всей доступной информацией. Они могут вносить коррективы в свои ожидания на краткосрочных временных интервалах. Их реакция будет выражаться в изменении условий продажи факторов производства в соответствии с оценкой ожидаемой инфляции. Поэтому любые изменения в совокупном спросе будут сопровождаться одновременным изменением совокупного предложения; и уровень выпуска, и занятость не изменятся. Графически это можно интерпретировать как одновременное смещение краткосрочных кривых AD и AS (рис. 2.23, а). Поэтому краткосрочная кривая Филлипса представлена вертикальной линией, совмещенной с долгосрочной кривой Филипса.
В концепции рациональных ожиданий отсутствует проблема альтернативности объема производства и инфляции: совокупное предложение не изменится при росте уровня цен в долгосрочном периоде, а краткосрочная кривая Филлипса совпадает с вертикальной прямой на уровне естественной безработицы (рис. 2.23, б).
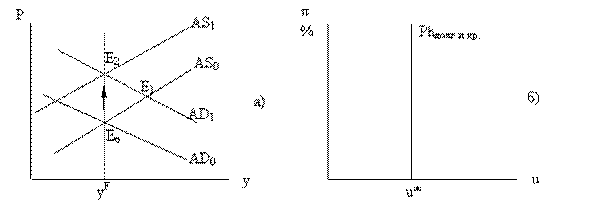
Рисунок 2.23 – Кривая Филипса при рациональных ожиданиях
Экономические субъекты учитывают изменения конъюнктуры и действия правительства. Любые изменения в совокупном спросе (AD1 → AD0) сопровождаются одновременным изменением совокупного предложения (AS0 → AS1). Это предопределено тем, что экономические субъекты формируют и меняют свои планы по условиям продажи факторов производства. В результате не изменяются ни реальный ВВП, ни занятость. Поэтому кривая Филипса в краткосрочном и долгосрочном периодах вертикальна.
Важную роль в теории рациональных ожиданий играет доверие к правительству: если доверие существует, инфляция будет прогнозироваться на основе политических решений правительства, а не на прошлых представлениях. Ликвидации инфляции будут способствовать: отсутствие долгосрочных соглашений о заработной плате; рациональность ожиданий экономических субъектов; кредит доверия правительства.
Модель формирования рациональных ожиданий в теории рациональных ожиданий критикуется как не соответствующая реальности. При образовании рациональных ожиданий должен учитываться тот факт, что информация о будущем имеет высокую цену. Прогнозы на будущее могут быть оптимальными не потому, что являются точными, а потому, что сбор более подробной информации слишком дорог. По мнению представителей маржинализма и кейнсианства, ссылающихся на фундаментальную непредсказуемость будущего, формирование ожидаемого не может быть рациональным. Так как экономические субъекты не обладают полнотой информации, в рамках гипотезы рациональных ожиданий нельзя решить проблему построения реальных подтверждаемых прогнозов.
§
3.1 Модели финансовых «пузырей»
3.2 Политика центрального банка в моделях инфляционного целеполагания и ограничения кредитной эмиссии
3.3 Модель Баумоля – Тобина трансакционного спроса (управления наличностью)
3.4 Концепция финансовой хрупкости Х. Мински
3.5 Модель неверных представлений Фридмана – Фелпса в теории инфляции
3.6 Модель Кэгана в теории инфляции
3.7 Модель Саржента – Уоллеса в теории инфляции
3.8 Модель Кидланда – Прескотта несостоятельности политики низкой инфляции
3.9 Модель делегирования полномочий в политике низкой инфляции
3.10 Модели динамики государственного долга
3.11 Оценка последствий государственного долга. Теорема эквивалентности Рикардо – Барро
3.12 Модели платежеспособности государства по внутреннему долгу
3.13 Модели платежеспособности государства по внешнему долгу
3.14 Условие общей платежеспособности государства. Критические значения платежеспособности
3.15 Модель Бруно-Фишера эмиссионного финансирования дефицита бюджета
3.16 Модель Бруно-Фишера смешанного финансирования дефицита бюджета
Модели финансовых «пузырей»
Под денежно-кредитной политикой подразумевается воздействие на экономическую конъюнктуру посредством регулирования количества находящихся в обращении денег на денежном рынке Главным проводником этой политики является Центральный банк, ответственный за обеспечение страны необходимым для эффективного функционирования экономики количеством денег. Основной проблемой современного денежного рынка является риск возникновения финансовых «пузырей».
Финансовый «пузырь» – существенное отклонение (значительное и длительное превышение) текущей рыночной цены актива от его фундаментальной стоимости, как правило на фондовом рынке и рынке недвижимости. Финансовый «пузырь» возникает в результате ажиотажного спроса на товар, что приводит, в конечном итоге, к кризису – к одномоментному и резкому падению цены.
«Пузырь» может быть вызван локальным самоподдерживающимся и усиливающимся подражанием среди трейдеров – участников денежного рынка. Тенденция подражания усиливается до определенной точки, называемой «критической». В критический момент множество трейдеров могут разместить приказы на продажу, которые не находят встречного спроса, что в свою очередь приводит к финансовому краху.
Финансовый «пузырь» не всегда заканчивается крахом, поэтому рациональным поведением трейдеров и инвесторов остается стратегия удержания позиции, при условии, что риск краха компенсируется высокими темпами роста пузыря.
Модель финансового «пузыря» в общем виде представляется следующим образом (рис. 3.1).

Рисунок 3.1 – Модель финансового «пузыря»
Процесс развития рыночной экономики – это череда их «надувания» и «схлопывания». Каждое «лопание пузыря» возвращает рынок и экономику на долгосрочный плавно-восходящий тренд (фаза Smart Money на рис. 3.1).
С фундаментальной точки зрения, существует ряд предпосылок для «надувания» пузырей:
— низкие процентные ставки и высокая инфляция (австрийская школа);
— стимулирующая монетарная политика;
— быстрые темпы экономического роста;
— рост масштабов собственности и развитие инвестиционных фондов;
— развитие новых информационных технологий;
— многообещающие прогнозы аналитиков;
— создание эффекта наличия в стране свободных денег;
— опережающие темпы роста спроса по сравнению с ростом предложения.
Так, например, небольшая процентная ставка в экономике не способствует развитию инвестиций, ведь 1-2 % годовых непривлекательны для инвесторов. Поэтому, инвесторы с большим капиталом стараются вложить свои средства на бóльший период, не особо «вникая» в текущую стоимость активов. С другой стороны, если инфляция в стране средняя, то бдительность инвесторов усыпляется незначительным ростом заработной платы населения, возрастанием потребления, что все вместе уже «кормит» скрытый «пузырь» и ведет экономику к кризису (события 2007 года в преддверии мирового финансового кризиса).
Однако, если инфляция начинает становиться выше средней и превышает процентные ставки в стране, то инвесторам выгодно вкладывать свои средства в дорожающие товары и сырье.
Объективность возникновения финансового «пузыря» объясняется следующими обстоятельствами.
1. Существуют адекватные фундаментальные причины для роста цены актива.
2. Текущая цена на актив отражает фундаментальные факторы гипертрофированным образом, так что существует значительный разрыв между настоящей и фундаментально-обоснованной («справедливой») ценой.
3. Скопление спекулянтов на длинной стороне в течение длительного периода времени, так что совокупная спекулятивная позиция показывает значительную бумажную прибыль. Как бычий тренд, так и его фундаментальные причины хорошо осознаны большинством спекулянтов, они уже длительное время эксплуатируют бычий тренд и получают прибыль (главным образом – бумажную).
4. Доходность актива постепенно возрастает несколькими последовательными волнами, так что долгосрочный тренд принимает форму параболы. Поскольку по мере созревания пузыря уверенность спекулянтов в росте увеличиваются, кривая спекулятивного спроса стремится к вертикали (фаза Public на рис. 3.1).
В истории экономики выделяют следующие виды пузырей: спекулятивный (рыночный), рациональный, комиссионный и внутренний.
Рыночный пузырь происходит в случае отсутствия достаточного количества предложения активов для инвестиций в противовес большому спросу на деньги (активов мало – денег много).
Рациональный пузырь базируется на экономических идеях Р. Лукаса, который разработал теорию рациональных ожиданий. Лукас считал, что пузырь представляет собой разницу рыночной цены на товар и цены, которая складывается на основании фундаментальной оценки ее стоимости. Как только фундаментальная оценка стоимости товара не совпадает с ее рыночной ценой, сразу возникает пузырь и кризис.
Комиссионный пузырь характеризуется мотивацией портфельного менеджера по инвестициям осуществлять за счет клиентов множества сделок с целью получения большего размера вознаграждений. Как вы понимаете, менеджер постоянно покупает и продает различные активы, чтобы нагнать объем операций и за каждую получить себе причитающееся ему комиссионное вознаграждение.
Внутренний пузырь связан с зависимостью пузыря от дивидендных выплат по акциям. Предполагается, что если на предприятии – эмитенте все хорошо, то пузырь не раздувается, зато, как только происходит переоценка активов предприятия, это сразу отражается на размере дивидендов акционеров, и пузырь раздувается. Это обстоятельство ведет экономику к кризису.
Сложность предвидения возникновения финансовых «пузырей» связана, как правило, с тем, что в рыночной экономике сложно заранее определить справедливую стоимость товаров, поэтому пузырь обнаруживают уже только после его возникновения.
Как показывает опыт экономистов, спрогнозировать надувание очередного финансового «пузыря» оказывается на практике очень тяжело. Если Центральный банк страны и может отследить излишний спрос на определенные активы, то вмешательство в рыночный механизм функционирования экономики обычно нежелательно: иногда действия по ограничению деятельности игроков, контролю объема финансовых операций, регулированию процентных ставок могут привести к большему финансовому кризису.
Предположим, типичный инвестор в экономике имеет возможность выбора: вкладывать средства в реальный сектор, выражаемый объемом капитальных инвестиций к, или приобретать актив, показывающий свойства спекулятивного роста, который может перейти в финансовый пузырь.
Если инвестор выбирает капитальный (неспекулятивный) актив в период г, его доходность в следующий период (1 0 будет равна предельной производительности капитала: 1 /'(.к[ 1), где/Хк1 1) — первая частная производная производственной функции по капиталу. Если инвестор приобретает спекулятивный актив по цене Р( с тем, чтобы перепродать по цене Р( 1, его доходность за этот же период времени составит Р, 1/Р,. Принцип арбитража предполагает выравнивание доходности спекулятивного и неспекулятивного активов с течением времени для преобладающего числа инвесторов в экономике. Поэтому получаем равенство:
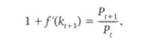
Обозначим через В1 = МР1 общую стоимость спекулятивных активов в экономике, М — число спекулятивных активов. Тогда, учитывая арбитражное уравнение, запишем прирост стоимости спекулятивного актива в следующий период:

Модифицируем полученное выражение таким образом, чтобы получить данные на душу населения:
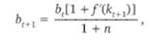
где Ьг — стоимость спекулятивных активов в экономике на душу населения в начальный период; Ь[ 1 — стоимость спекулятивных активов в экономике на душу населения в конечный период времени; п — темп прироста населения страны.
Пузырь начинает надуваться в тот момент, когда/'(к) > п, предельная производительность капитала начинает превышать темп прироста населения.
Когда в экономике присутствуют спекулятивные активы, часть сбережений населения расходуется непроизводительно, что сокращает накопление капитала на душу населения:
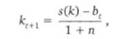
где к1 х — объем капитала (реальных активов) на душу населения в конечный период времени; ¿(/0 — функция сбережений на душу населения.
Эти два уравнения задают зависимость, которая может быть названа «функцией финансового пузыря» (рис. 8.9).
Развитие экономики, в принципе, возможно и без образования финансовых пузырей (в точке, где Ь( = 0). Однако если пузырь начинает формироваться, остановить его достаточно сложно, поскольку на его поддержку направляются сбережения населения, и пока весь текущий запас сбережений не будет исчерпан (или близок к исчерпанию), подпитка пузыря будет продолжаться.
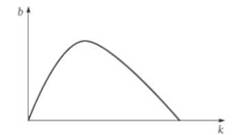
Рисунок 3.2 — Функция финансового пузыря
§
Поскольку денежно-кредитная политика воздействует на реальный сектор экономики посредством регулирования конъюнктуры денежного рынка, то для достижения конечных целей стабилизационной политики Центральному банку приходится реализовывать промежуточные цели в виде поддержания на определенном уровне количества денег, ставки процента или обменного курса национальной валюты. Как и конечные, промежуточные цели денежной политики часто находятся в отношении субституции; отсюда возникает дилемма промежуточных целей. В закрытой экономике она сводится к вопросу, что следует выбирать центральному банку в качестве объекта регулирования – ставку процента или денежную массу? Если при изменении спроса на деньги не изменять их предложение, то будет колебаться ставка процента, а для поддержания ставки процента на неизменном уровне необходимо менять предложение денег вслед за изменением спроса на них.
До 70-х гг. ХХ в. в развитых странах рыночной экономики преобладала практика поддержания стабильной ставки процента для предотвращения колебаний инвестиционного спроса, приводящих к возникновению конъюнктурных циклов. В 1970-х гг. ФРС США и центральные банки западноевропейских стран переориентировались на стабилизацию денежной массы. Этому содействовали две причины: ускоренное развитие инфляции, переросшей в стагфляцию, и широкое распространение учения монетаристов о роли денег.
Кроме того, в 80-х гг. ХХ в. в связи с существенным обогащением ассортимента финансовых инструментов (финансовых инноваций) и глобализацией валютных операций обнаружилась нестабильность спроса на деньги. Поэтому с 1980-х гг. стала проводиться более свободная денежная политика, в ходе которой выбор промежуточной цели определяется текущей экономической конъюнктурой. Так, благодаря оперативному удовлетворению резко возросшего спроса населения на деньги после крупнейшего обвала цен на Нью-Йоркской фондовой бирже 19 октября 1987 г. удалось избежать серьезных потрясений финансовой системы США. ФРС пошла на увеличение предложения денег, несмотря на то что экономика страны в то время находилась в состоянии полной занятости.
В 1990-х гг. во многих странах основной целью денежно-кредитной политики стало удержание темпов инфляции в заранее провозглашенных пределах (таргетирование инфляции).
При проведении денежно-кредитной политики необходимо учитывать различие между краткосрочной и долгосрочной ставками процента. Мероприятия денежной политики непосредственно определяют величину краткосрочной ставки, которая устанавливается на денежном рынке. В то же время на конъюнктуру рынка благ влияет долгосрочная ставка процента, определяющая спрос на инвестиции в реальный капитал. Поэтому денежно-кредитная политика лишь в том случае отразится на реальном секторе экономики, если приведет к изменению величины долгосрочной ставки процента.
Для регулирования экономической конъюнктуры государство может одновременно применять инструменты и фискальной, и денежной политики.
Для комплексного представления последствий стабилизационной политики государства в концепции «новых классиков» (Р. Лукас и др.) используется макроэкономическая модель, состоящая из двух дифференциальных уравнений – динамических функций совокупного спроса и совокупного предложения
YtD = At h∙(Mt – πt) ωt, (3.1)
YtS = yе g∙(nt – πt*) νt, (3.2)
гдеAt – независимый от реальной кассы спрос на блага, включая государственные расходы;
h и g – коэффициенты согласования размерности;
ωt и νt – стохастические переменные с нулевым ожиданием, представляющие все неучтенные в модели случайные факторы формирования совокупного спроса и предложения.
Благодаря гибкости цен правые части равенств всегда равны друг другу.
В соответствии с концепцией рациональных ожиданий
ytDe = At h∙(M – πe). (3.3)
Таким образом, из модели новых классиков следует, что текущая величина национального дохода отклоняется от своего значения при полной занятости по двум причинам: из-за случайных экзогенных шоков и вследствие непредвиденных мероприятий стабилизационной политики. Но каков бы ни был объем производства, благодаря гибкости цен совокупный спрос всегда равен совокупному предложению. Экономика всегда находится в равновесном состоянии, хотя величина национального дохода подвержена конъюнктурным колебаниям.
Ожидаемое значение темпа инфляции формируется на основе намерений правительства. При отсутствии непредвиденных обстоятельств ( ωt = νt = 0) и неожиданных мероприятий стабилизационной политики правительства, фактический темп инфляции равен ожидаемому, а объем производства – величине национального дохода полной занятости. Любое непредвиденное событие, будь то экзогенные шоки технического прогресса или мероприятия экономической политики, отклоняют фактические значения от ожидаемых. При случайном повышении совокупного спроса ( 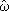 t > 0) уровень цен повышается; в случае непредвиденного роста совокупного предложения (
t > 0) уровень цен повышается; в случае непредвиденного роста совокупного предложения (  t > 0) темп инфляции снижается.
t > 0) темп инфляции снижается.
Когда государство не проводит активной стабилизационной политики, тогда величина национального дохода колеблется около значения национального дохода полной занятости, а уровень цен растет или понижается в зависимости от того, возникают ли экзогенные шоки на стороне спроса или предложения, и от того, положительные или отрицательные значения принимают параметры  t и
t и  t.
t.
Таким образом, из модели новых классиков следует, что текущая величина национального дохода отклоняется от своего значения при полной занятости по двум причинам: из-за случайных экзогенных шоков и вследствие непредвиденных мероприятий стабилизационной политики. Но каков бы ни был объем производства, благодаря гибкости цен совокупный спрос всегда равен совокупному предложению. Экономика всегда находится в равновесном состоянии, хотя величина национального дохода подвержена конъюнктурным колебаниям.
§
Модель управления наличной денежной массой была разработана в 50-х годах ХХ в. американскими экономистами У. Баумолем и Дж. Тобином и получила название «модель Баумоля – Тобина».
Модель определяет оптимальное число посещений банка или оптимальную сумму наличных денег, исходя из соотношения убытков в виде неполученного на эту сумму банковского процента и стоимостной оценки экономии времени от более редких походов в банк.
Предположим, что вы решили израсходовать за год Y денежных единиц. При допущении постоянства цен у вас есть несколько вариантов поведения:
1) снять всю сумму в Y денежных единиц со счета и держать ее в виде наличных денег на руках в течение всего года;
2) снимать сумму в Y денежных единиц со счета частями в течение года.
Очевидно, в первом варианте значительными будут потери в виде неполученного процента по вкладам, в то же время, во втором варианте при посещении банка более одного раза возрастают издержки, связанные с самим посещением банка (дорога в банк и обратно, потеря времени на стояние в возможной очереди в банке и т.п.), что получило название «издержки стоптанных башмаков».
Если выбирается второй вариант, то возникает вопрос об оптимальном среднем количестве наличных денег на руках и оптимальном числе посещений банка.
Среднее количество наличных денег на руках в первом варианте в течение года будет Y:2 (Y ден. ед. в начале года, 0 – в конце года), количество посещений банка – одно.
Если два раза в год индивид посещает банк и снимает сумму в Y/2 ден. ед. два раза, то среднее количество денег на руках в течение года будет Y/4 (Y/2 — в начале года и 0 — в конце года).
Если четыре раза клиент посещает банк и снимает сумму в Y/4 ден. ед. четыре раза в год, то среднее количество наличных денег на руках в течение года будет Y / 8 и т.п. При N походах в банк и снятии каждый раз сумм в Y / N ден. ед. среднее количество наличных денег на руках в течение года будет Y / 2 N ден. ед.
Чем меньше будет сумма в Y / 2 N ден. ед., тем меньше будут потери в виде недополученного процента по возможному вкладу, но тем больше будут издержки, связанные с посещением банка.
Как выбирается оптимальное число посещений банка (N*)?
Пусть «издержки стоптанных башмаков» на одно посещение банка составят F ден. ед., а ставка процента по вкладу — I, тогда потери в виде недополученного процента по вкладу будут равны произведению средней величины наличных денег на руках в течение года на процентную ставку: Y / 2N • I. Общая сумма издержек на посещение банка — F • N. Тогда совокупные издержки будут равны:
C = Y / 2N • 1 FN.
Как только издержки на посещение банка (FN) начинают превышать сумму недополученных процентов (Y / 2N • i), совокупные издержки (С) возрастают.
При N = N* кривая издержек на посещение банка и кривая недополученных процентов пересекаются в точке В, где издержки на посещение банка и издержки, связанные с недополученным процентом, равны:
FN* = 2N* • i.
Отсюда:
N* = ¥ iY / 2F .
При N = N* средняя сумма наличных денег на руках в течение года составит:
М = Y / 2N* = Y / (2 ¥ Yi / 2F)/,
Упрощая это выражение, получаем:
М2 = Y2 • 2F / 4Yi = YF / 2i ⇒ ¥ М = YF / 2i/.
Следовательно, население имеет наличных денег на руках тем больше, чем выше издержки, связанные с посещением банка (F), чем больше сумма, которую человек запланировал потратить в течение года (Y), и чем меньше процентная ставка.
Модель Баумоля – Тобина можно использовать также при наборе оптимального варианта распределения богатства на активы в денежной форме и на неденежные активы в форме акций и облигаций.
В этом случае i — разность доходов от хранения богатства в виде денежных и неденежных активов, a F — затраты на преобразование неденежных активов в денежные (например, затраты на брокерские услуги), а N — количество таких преобразований в год.
Кроме того, модель Баумоля – Тобина показывает, что спрос на наличные деньги прямо пропорционален (Y) и обратно пропорционален ставке процента (i).
§
Кривая IS («инвестиции – сбережения») описывает равновесие на товарном рынке и отражает взаимоотношения между рыночной ставкой процента r и уровнем дохода Y. Кривая IS выводится из простой кейнсианской модели (модели равновесия совокупных расходов или модели кейнсианского креста), но отличается тем, что часть совокупных расходов и, прежде всего, инвестиционные расходы теперь зависят от ставки процента. Ставка процента перестает быть экзогенной переменной и становится эндогенной величиной, определяемой ситуацией на денежном рынке, т.е. внутри самой модели. Зависимость части совокупных расходов от ставки процента имеет результатом то, что для каждой ставки процента существует точное значение величины равновесного дохода и поэтому может быть построена кривая равновесного дохода для товарного рынка – кривая IS. Во всех точках кривой IS соблюдается равенство инвестиций и сбережений. Термин IS отражает это равенство (Investment = Savings).
Простейший графический вывод кривой IS связан с использованием функций сбережений и инвестиций (рис. 14).
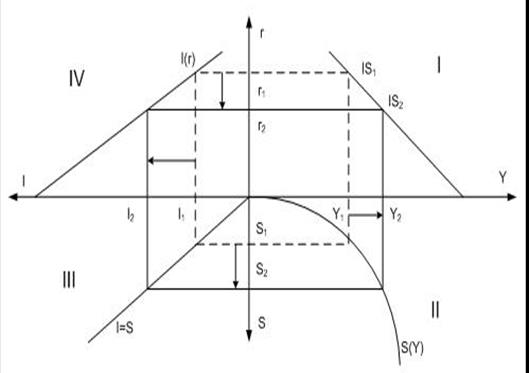
Рис. 14.Графический вывод кривой IS
В квадранте II представлен график функции сбережений S(Y): с ростом дохода Y1 до Y2 сбережения увеличиваются с S1 до S2.
В квадранте III представлен график I=S (линия под углом в 45° к осям координат I и S). I1 = S1, I2 = S2.
В квадранте IV представлен график функции инвестиций I=I(r), показывающий рост инвестиций как функцию, обратную уровню процентной ставки r.
На основе этих данных в квадранте I находим множество равновесных сочетаний Y и r, т.е. кривую IS: IS1(Y1, r1) и IS2(Y2, r2), чем ниже ставка процента, тем выше уровень дохода.
Аналогичные выводы могут быть получены с использованием модели Кейнсианского креста (рис. 15).
График инвестиций (рис. 15, I) показывает, что низкие ставки процента соответствуют высокому уровню инвестиций. При уровне процентной ставки r1 объем плановых инвестиций будет I1. Соответственно, совокупные расходы Е1 (рис. 15, II) показаны линией С I1 (r1) G, которая, пересекаясь с биссектрисой, определяет точку равновесия Е1 и равновесный объем национального дохода Y1. Таким образом, при процентной ставке r1 равновесным будет национальный доход Y1. Эти параметры определят точку A (рис. 15, III). Если процентная ставка повышается с r1 до r2, инвестиции уменьшаются с уровня I1 до I2 (рис. 15, I), кривая совокупных расходов сдвигается вниз, в положение С I2 (r2) G (рис. 6.2, II). Это, в свою очередь, снижает уровень равновесия национального дохода с Y1 до Y2 (рис. 15, III). Эти параметры определят точку В. Если непрерывно изменять значения процентной ставки и для каждого находить соответствующие значения национального дохода, то получим кривую IS (рис. 15, III).
Движение вдоль кривой IS показывает, как должен измениться уровень национального дохода при изменении уровня процентной ставки для того, чтобы на рынке благ сохранилось равновесие.
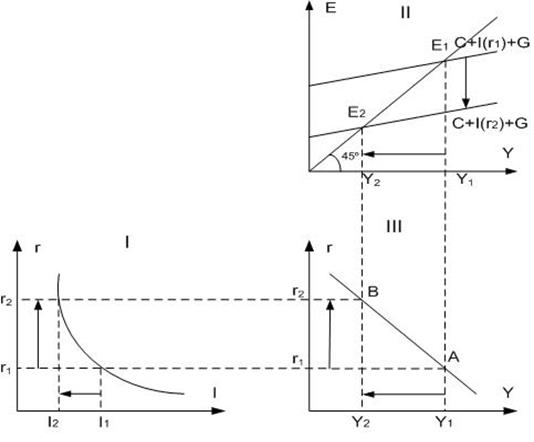
Рис. 15.Графический вывод кривой IS из модели Кейнсианского креста
Кривая IS имеет отрицательный наклон, т.е. выпуск, уравновешивающий рынок товаров, падает с ростом ставки процента. Более высокий уровень ставки процента вызывает уменьшение инвестиционных и потребительских расходов, и, следовательно, совокупного спроса (совокупных расходов), что ведет к более низкому уровню равновесного дохода (рис. 16).
Рис. 16. Кривая IS
Кривая IS разбивает экономическое пространство на две области. Во всех точках, лежащих выше, предложение товаров больше спроса на них, т.е. объем национального дохода больше запланированных расходов. В точке А совокупный выпуск Y1 больше, чем равновесный. Этот излишек предложения товаров ведет к незапланированному накоплению запасов, в результате чего снижается объем выпуска и экономика двигается по направлению к кривой IS. Во всех точках ниже кривой IS наблюдается дефицит на рынке благ. В точке В объем совокупного выпуска Y2 ниже равновесного. Избыточный спрос ведет к незапланированному уменьшению запасов, что предполагает рост объема выпуска и смещение по направлению к кривой IS. Таким образом, кривая IS соединяет точки, в которых общее количество произведенных товаров равно общему объему спроса на них.
Сдвиги кривой IS обусловлены изменениями любого из компонентов расходов C, I, G и налогов T. Все, что увеличивает расходы (оптимизм предпринимателей и потребителей, усиливающий их желание увеличивать расходы при любой ставке процента, что ведет к росту потребительских и инвестиционных расходов; рост государственных расходов; снижение аккордных налогов; увеличение трансфертных выплат) сдвигает кривую IS вправо, и наоборот.
Таким образом, кривая IS сдвигается из положения IS1 в положение IS2 (рис. 17) в результате:
— увеличения потребительских расходов;
— увеличения плановых инвестиций (не связанных с изменением процентной ставки);
— увеличение государственных расходов;
— снижения налогов.
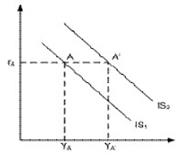
Рис. 17. Cдвиги кривой IS
Угол наклона кривой IS определяется двумя факторами: мультипликатором государственных расходов и чувствительностью инвестиций к ставке процента.
Поскольку коэффициент при G (мультипликатор государственных расходов) положителен, рост государственных расходов сдвигает кривую IS вправо, а коэффициент при T (налоговый мультипликатор) отрицателен и рост налогов сдвигает кривую IS влево. Кроме того, чем больше предельная склонность к потреблению, тем больше величина мультипликатора, и, следовательно, больше сдвиг кривой IS. Кривая IS сдвигается на меньшее расстояние при изменении налогов, чем при изменении на такую же величину государственных расходов.
Равновесие денежного рынка
Кривая LM («предпочтение ликвидности – денежная масса») показывает все возможные соотношения Y и r, при которых спрос на деньги равен предложению денег. Термин LM отражает это равенство: L (Liquidity Preference) обозначает предпочтение ликвидности, кейнсианский термин для обозначения спроса на деньги, а М (Money Supply) – предложение денег.
В основе построения кривой LM лежит кейнсианская теория предпочтения ликвидности, объясняющая, как соотношение спроса и предложения реальных запасов денежных средств определяют ставку процента. Реальные запасы денежных средств представляют собой номинальные запасы, скорректированные на изменение уровня цен и равные М/Р. В соответствии с теорией предпочтения ликвидности, предложение реальных денежных средств фиксировано и определяется центральным банком. Рассмотрим построение кривой LM на основе графического анализа равновесия денежного рынка.
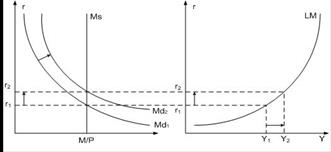
Рис. 18.Графический вывод кривой LM (первый способ)
На рис.18 кривая предложения денег – вертикальная линия, соответствующая заданному реальному количеству денег в экономике. Пересечение кривой спроса с кривой предложения денег дает нам ставку процента r1, которая уравновешивает рынок денег при данном уровне дохода Y1. Если доход увеличится до уровня Y2, то кривая спроса на деньги сдвинется вправо, более высокому уровню доходов соответствует более высокая равновесная ставка процента r2. Совокупность всех пар (Y, r), которые уравновешивают рынок денег, даст нам кривую LM.
Точно так же, как экономика стремится к точкам равновесия, лежащим на кривой IS, она стремится и к точкам равновесия, определяемым кривой LM (рис. 19).
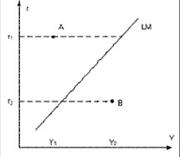
Рис. 19. Кривая LM
Если экономическая ситуация соответствует точке слева (сверху) от кривой LM (точка А), то можно говорить об избыточном предложении денег. У людей оказывается больше денег, чем они желают иметь. Для того чтобы избавиться от «лишних» денег, они будут, например, покупать облигации, это повлечет за собой повышение цен на облигации и снижение процентных ставок. При избыточном предложении денег ставка процента будет падать до тех пор, пока не достигнет равновесного уровня, задаваемого кривой LM.
Если экономика описывается точкой справа (снизу) от кривой LM, то можно говорить об избыточном спросе на деньги. В точке В люди хотят иметь больше денег, чем у них есть. Для этого они будут продавать облигации, тем самым снизится их цена и повысится процентная ставка. Этот процесс будет продолжаться до тех пор, пока процентная ставка не повысится до равновесного уровня, определяемого точкой на кривой LM.
Следует отметить, что кривая LM, так же как и кривая IS, не выражает функциональную зависимость национального дохода от ставки процента или, наоборот, а определяет все возможные комбинации сочетаний равновесных значений дохода и ставки процента.
§
Кривая IS отражает все соотношения между Y и r, при которых товарный рынок находится в равновесии. Кривая LM – все комбинации Y и r, которые обеспечивают равновесие денежного рынка. Пересечение кривых IS и LM дает единственные значения величины ставки процента r* (равновесная ставка процента) и уровня дохода Y* (равновесный уровень дохода), обеспечивающие одновременное равновесие на товарном и денежном рынках. Равновесие в экономике достигается в точке Е (рис. 20).

Рис. 20.Равновесие в модели IS – LM
На рис. 20 (например, в точке А, которая лежит на кривой IS, но вне кривой LM) существует равновесие на товарном рынке (т.е. совокупный выпуск равен совокупному спросу). В этой точке процентная ставка оказывается выше равновесной, поэтому спрос на деньги меньше, чем их предложение. Так как у людей есть лишние деньги, они попытаются избавиться от них, купив облигации. В результате увеличатся цены на облигации, что приведет к падению процентных ставок, а это, в свою очередь, приведет к росту планируемых инвестиционных расходов. Таким образом, совокупный спрос вырастет. Точка, описывающая состояние экономики, движется вниз по кривой IS до тех пор, пока процентная ставка не упадет, а совокупный выпуск не вырастет до равновесного уровня.
В случае если экономическая ситуация описывается точкой, лежащей на кривой LM, но вне кривой IS (точки В и D), рыночные механизмы все равно приведут ее к равновесию. В точке В несмотря на то, что спрос на деньги равен их предложению, совокупный выпуск оказывается выше равновесного уровня, больше совокупного спроса. Фирмы не могут продать свою продукцию и накапливают незапланированные запасы, что заставляет их сокращать производство и снижать выпуск. Снижение объема производства означает, что спрос на деньги упадет, все это приведет к снижению процентных ставок. Точка, описывающая состояние экономики, будет двигаться вниз по кривой LM до тех пор, пока не достигнет точки общего равновесия.
4. Модель IS-LM и построение кривой совокупного спроса
Графический инструментарий модели IS-LM позволяет проанализировать влияние различных вариантов макроэкономической политики на совокупный спрос и рассмотреть, как каждое планируемое изменение в политике воздействует на равновесный уровень дохода.
Кривые IS и LM могут изменять свое положение под воздействием различных факторов, из которых наибольший интерес представляют изменения государственных расходов, налогов и предложения денег, поскольку они являются инструментами фискальной и денежно-кредитной политики. В модели IS-LM воздействие фискальной политики будет отражаться в сдвигах кривой IS, а денежно-кредитной – в сдвигах кривой LM.
Влияние фискальной политики
Рассмотрим сдвиг кривой IS, вызванный ростом государственных расходов. Предположим, что первоначально равновесие на рынках товаров и денег достигалось в точке Е1 при процентной ставке r1 и национальном доходе Y1 (рис. 21).
Допустим, экономическая ситуация в стране потребовала увеличения государственных расходов. Они приводят к увеличению совокупных расходов, что обусловливает рост национального объема производства, кривая IS1 сдвигается в положение IS2.
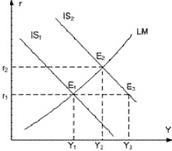
Рис. 21. Стимулирующая фискальная политика в модели IS – LM
Но растущий совокупный выпуск увеличивает спрос на деньги, который начинает превышать предложение денег, что, соответственно, приводит к росту процентной ставки до r2. На товарном рынке увеличение совокупных расходов побуждает предпринимателей увеличивать объем инвестиций. В свою очередь, рост процентной ставки начинает сдерживать этот процесс, заставляя предпринимателей сокращать планируемый при процентной ставке r1 прирост инвестиций. В этом случае новое положение равновесия на рынках товаров и денег будет достигнуто в точке Е2, а совокупный выпуск увеличится до Y2.
Прирост государственных расходов частично вытесняет плановые инвестиции, т.е. оказывает влияние эффект вытеснения. Этот эффект снижает эффективность стимулирующей фискальной политики. Именно на него ссылаются монетаристы, утверждая, что фискальная политика недостаточно действенна и приоритет в макроэкономическом регулировании должен быть отдан денежно-кредитной политике.
Снижение налогов при неизменном уровне государственных расходов оказывает такое же воздействие, как и увеличение государственных расходов. Оно приводит к тому, что при любом данном значении процентной ставки совокупный выпуск будет больше вследствие роста располагаемого дохода, потребления и совокупного спроса. Величина этого воздействия определяется налоговым мультипликатором. Однако равновесный уровень дохода также меньше, чем в модели Кейнсианского креста за счет повышения ставки процента.
Таким образом, влияние денежного рынка снижает мультипликативный эффект, однако в какой степени это происходит, зависит от того, в пределах какого из трех участков кривой LM происходит сдвиг кривой IS (рис. 22).

Рис. 22. Мультипликативный эффект на различных участках кривой LM
Если первоначальное совместное равновесие на рынках товаров и денег представлено на кейнсианском отрезке, то мультипликативный эффект дополнительных государственных расходов проявляется в полной мере (прирост дохода практически равен расстоянию сдвига кривой IS). Это объясняется тем, что в исходном состоянии равновесие установилось при низком уровне национального дохода и близкой к минимальной ставке процента. В подобной ситуации у людей небольшой спрос на деньги для сделок и большой спрос на них со стороны активов. Если при таком состоянии экономики начинает расти совокупный выпуск, то возникающая дополнительная потребность в деньгах для сделок удовлетворяется за счет денег, находящихся в активах, не вызывая существенного роста ставки процента, и планируемый объем инвестиций не будет сокращен.
Последствия сдвига линии IS на промежуточном участке кривой LM проанализированы на рис. 21.
Если совместное равновесие на рынках товаров и денег приходится на классический отрезок кривой LM, сдвиг линии IS вообще не изменит совокупный спрос на блага в текущем периоде. Причина заключается в том, что при ставке процента выше максимальной в составе активов домашних хозяйств уже нет денег, поэтому осуществить новые инвестиционные вложения можно только за счет перераспределения существующего объема кредитных средств к более эффективным вариантам. В результате суммарный инвестиционный спрос не изменится, а, следовательно, останется прежним и совокупный выпуск текущего периода.
Таким образом, стимулирующая фискальная политика (увеличение государственных расходов и снижение налогов) сдвигает кривую IS вправо (вверх), что увеличивает уровень дохода и ставку процента. Наоборот, сдерживающая фискальная политика (сокращение государственных расходов и увеличение налогов) сдвигает кривую IS влево, что сокращает доход и уменьшает ставку процента.
Влияние денежно-кредитной политики
Пусть первоначально экономика находится в состоянии равновесия в точке Е1 (рис. 23). Предположим, что правительство решает снизить уровень безработицы, увеличить объем совокупного выпуска путем увеличения предложения денег. Увеличение предложения денег сдвигает кривую LM вправо (вниз), в результате процентная ставка падает с r1 до r2, величина дохода растет с Y1 до Y2.
Рост предложения денег (сдвиг кривой LM в положение LM2) создает избыточное предложение на рынке денег, в результате чего ставка процента снижается. Ее падение вызывает рост инвестиционных расходов, приводящий к росту спроса на товары и услуги, увеличению совокупного выпуска.
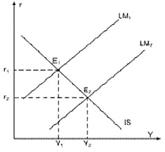
Рис. 23. Стимулирующая денежно-кредитная политика в модели IS – LM
Совместное равновесие рынка товаров и денег перемещается в точку Е2, поскольку рост дохода и снижение процентной ставки влекут за собой рост спроса на деньги, который будет продолжаться до тех пор, пока не сравняется с новым, более высоким уровнем предложения денег.
Снижение предложения денег предполагает обратный процесс: сдвиг кривой LM влево, рост ставки процента, снижение объема выпуска.
Степень влияния денежно-кредитной политики на экономику также зависит от наклона кривых IS и LM. При изменении предложения денег на одинаковую величину эффект снижения ставки процента будет тем больше, чем более крутая кривая LM, т.е. ставка процента снизится тем больше, чем менее чувствителен спрос на деньги к изменению ставки процента. Если кривая IS более пологая, что означает высокую чувствительность расходов к изменению ставки процента и большую величину мультипликатора государственных расходов, то достаточно очень незначительного снижения ставки процента, чтобы существенно увеличились расходы, мультипликативно увеличив доход. Эффективность денежно-кредитной политики тем больше, чем кривая LM более крутая, а кривая IS более пологая.
Таким образом, стимулирующая денежно-кредитная политика, инструментом которой выступает увеличение предложения денег (сдвиг вправо (вниз) кривой LM), ведет к росту уровня дохода и снижению ставки процента. Результатом сдерживающей денежно-кредитной политики (сдвиг влево (вверх) кривой LM), основанной на сокращении предложения денег, является снижение дохода и рост ставки процента.
Взаимодействие фискальной и денежно-кредитной политики
При анализе любого изменения в денежно-кредитной или фискальной политике важно иметь в виду, что инструменты одной политики могут влиять на результаты другой.
Предположим, что правительство озабочено бюджетным дефицитом, и решило увеличить налоги. Рассмотрим, какое влияние эта политика окажет в целом на экономику. В соответствии с моделью IS-LM, результаты будут зависеть от того, какую политику будет проводить Центральный банк в ответ на увеличение налогов. Возможно несколько вариантов.
1. Центральный банк поддерживает предложение денег на постоянном уровне (рис. 24а). Увеличение налогов сдвигает кривую IS влево (вниз) в положение IS2. В результате уменьшается совокупный выпуск (более высокие налоги уменьшают потребительские и инвестиционные расходы) и ставка процента (более низкий доход уменьшает спрос на деньги).
2. Центральный банк поддерживает ставку процента на постоянном уровне (рис. 24, b). В этом случае увеличение налогов также сдвигает кривую IS влево (вниз) в положение IS2, при этом центральный банк уменьшает предложение денег, чтобы процентная ставка оставалась на первоначальном уровне, кривая LM сдвигается в положение LM2. Доход сокращается на величину большую, чем на рисунке 24, а. В первом случае более низкая процентная ставка стимулирует инвестиции и частично возмещает эффект увеличения налогов. В данном случае центральный банк, поддерживая ставку процента на высоком уровне, углубляет спад в экономике.
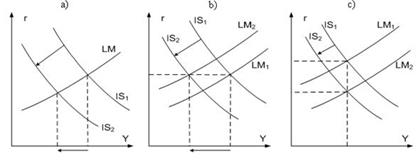
Рис. 24.Взаимодействие фискальной и денежно-кредитной политики в модели IS-LM
3. Центральный банк увеличивает предложение денег, чтобы сохранить уровень дохода на постоянном уровне (рис. 24, c). Увеличение налогов не повлечет за собой падение совокупного выпуска, поскольку кривая LM сдвигается вниз в положение LM2, чтобы возместить сдвиг кривой IS (более высокие налоги уменьшают потребление, в то же время более низкая процентная ставка стимулирует инвестиции). В этом случае увеличение налогов способствует падению ставки процента.
Данный пример иллюстрирует то, что результаты воздействия фискальной политики зависят от политики Центрального банка, т.е. поддерживает ли он предложение денег, ставку процента, или уровень дохода на постоянном уровне.
Комбинируя фискальную и денежно-кредитную политику, можно добиваться решения более сложных задач, чем простое регулирование объема выпуска (например, не изменяя объем выпуска, изменить его структуру). Подобная задача может быть весьма актуальна, если экономика находится в ситуации полной занятости и, следовательно, изменение выпуска нежелательно, однако его структура может требовать изменения.
В модели IS-LM выделяют особые случаи, когда один из видов политики не оказывает никакого воздействия на экономику. Это происходит, когда кривая LM горизонтальна, что соответствует ситуации «ликвидной ловушки»; кривая IS вертикальна, что соответствует ситуации «инвестиционной ловушки».
Экономика попадает в ситуацию ликвидной ловушки, когда процентные ставки настолько низки, что любое изменение денежного предложения поглощается спросом на деньги со стороны активов, уровень дохода падает до низшей отметки. Такая ситуация характерна для экономики, находящейся в состоянии депрессии.
Экономика попадает в ситуацию ликвидной ловушки, когда процентные ставки настолько низки, что любое изменение денежного предложения поглощается спросом на деньги со стороны активов, уровень дохода падает до низшей отметки. Такая ситуация характерна для экономики, находящейся в состоянии депрессии.
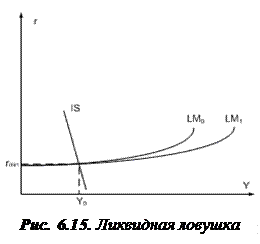 Графически это интерпретируется как пересечение кривых IS и LM в кейнсианской области кривой LM (рис. 6.15).
Графически это интерпретируется как пересечение кривых IS и LM в кейнсианской области кривой LM (рис. 6.15).
В ситуации ликвидной ловушки ставка процента минимальна, т.е. альтернативные издержки хранения наличных денег близки к нулю, и поэтому люди готовы держать любое количество денег, которое им будет предложено. В результате даже при нормальном отрицательном наклоне кривой IS увеличение предложения денег Центральным банком не способно обеспечить рост дохода. Обычно увеличение предложения денег снижает ставку процента, так как люди стараются избавиться от избытка денег, покупая облигации. Но если ставка процента находится на минимальном уровне, то цены на активы максимальны и люди стремятся их продать, опасаясь, что цены на них упадут, а их владельцы окажутся в проигрыше. В результате люди предъявляют безграничный спрос на деньги, отказываясь покупать ценные бумаги, и кривая спроса на деньги принимает горизонтальный вид. Это означает, что в функции спроса на деньги  коэффициент f, характеризующий чувствительность изменения спроса на деньги при изменении ставки процента, стремится к бесконечности. Кривая LM поэтому тоже горизонтальна, и изменение денежной массы не вызовет ее смещения. Прирост количества денег не сможет никого заставить приобретать ценные бумаги, вся сумма прироста предложения денег хранится в форме наличных денег. Величина дохода остается неизменной на уровне Y0. Стимулирующая денежно-кредитная политика не окажет никакого воздействия ни на ставку процента, ни на объем инвестиций, ни на уровень дохода, т.е. абсолютно неэффективна.
коэффициент f, характеризующий чувствительность изменения спроса на деньги при изменении ставки процента, стремится к бесконечности. Кривая LM поэтому тоже горизонтальна, и изменение денежной массы не вызовет ее смещения. Прирост количества денег не сможет никого заставить приобретать ценные бумаги, вся сумма прироста предложения денег хранится в форме наличных денег. Величина дохода остается неизменной на уровне Y0. Стимулирующая денежно-кредитная политика не окажет никакого воздействия ни на ставку процента, ни на объем инвестиций, ни на уровень дохода, т.е. абсолютно неэффективна.
В этом случае эффективность фискальной политики максимальна. Например, рост государственных закупок на 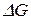 увеличивает равновесный доход на
увеличивает равновесный доход на 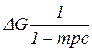 , т.е. эффект вытеснения отсутствует, доход возрастает на всю величину мультипликатора.
, т.е. эффект вытеснения отсутствует, доход возрастает на всю величину мультипликатора.
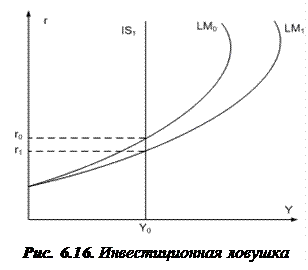 Другая ситуация получила название инвестиционной ловушки, соответствующая ситуации, при которой спрос на инвестиции совершенно неэластичен к ставке процента, поэтому график функции инвестиций приобретает вертикальный вид, а вертикальной кривой инвестиций соответствует вертикальная кривая IS (рис. 6.16).
Другая ситуация получила название инвестиционной ловушки, соответствующая ситуации, при которой спрос на инвестиции совершенно неэластичен к ставке процента, поэтому график функции инвестиций приобретает вертикальный вид, а вертикальной кривой инвестиций соответствует вертикальная кривая IS (рис. 6.16).
В результате любые изменения на денежном рынке, хотя и будут приводить к изменению ставки процента, но не вызовут изменения инвестиционного спроса. В этом случае чувствительность совокупных расходов к изменению ставки процента равна 0, и эффективной будет только фискальная политика. При этом эффективность фискальной политики максимальна, поскольку отсутствует эффект вытеснения и действует только эффект мультипликатора. Рост государственных расходов, вызывая увеличение совокупных расходов, ведет к росту спроса на деньги, что повышает ставку процента, но более высокая ставка не приводит к вытеснению расходов частного сектора, поскольку они не зависят от ставки процента. В результате фискального импульса наблюдается полный мультипликативный рост дохода. Денежно-кредитная политика совершенно неэффективна, поскольку снижение ставки процента (от r0 до r1) в результате увеличения предложения денег (сдвиг кривой LM вправо от LM0 до LM1) не повлияет на величину инвестиционных расходов, так как они совершенно нечувствительны к ее изменению.
Такая ситуация может возникнуть по самым разным причинам (например, она характерна для инфляционной экономики, когда ставки процента чрезмерно велики).
Следует иметь в виду, что ликвидная и инвестиционная ловушки имеют место только в кейнсианской модели. Если предположить, что поведение экономических субъектов описывается монетаристскими функциями, то возникает эффект имущества.
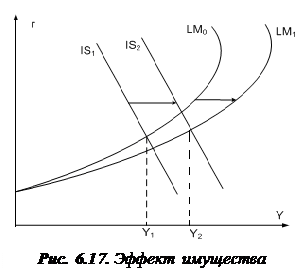 Эффект имущества заключается в том, что рост доли денег экономические субъекты воспринимают как нарушение оптимальной структуры портфеля активов, и как рост своего имущества. Поэтому избыток денег они стараются обменять не только на финансовые активы, но и на реальный капитал и реальные блага, что, в свою очередь, вызывает рост совокупного спроса. Рост совокупных расходов сдвигает кривую IS вправо, ликвидируя ловушки (рис. 6.17).
Эффект имущества заключается в том, что рост доли денег экономические субъекты воспринимают как нарушение оптимальной структуры портфеля активов, и как рост своего имущества. Поэтому избыток денег они стараются обменять не только на финансовые активы, но и на реальный капитал и реальные блага, что, в свою очередь, вызывает рост совокупного спроса. Рост совокупных расходов сдвигает кривую IS вправо, ликвидируя ловушки (рис. 6.17).
Изучение влияния стимулирующей денежно-кредитной или фискальной политики на модель IS-LM позволяет сделать вывод: денежно-кредитная и фискальная политика влияют на выпуск в краткосрочном периоде, но ни одна из них не влияет на объем выпуска в долгосрочном периоде. Важным моментом при оценке эффективности этих политик с точки зрения увеличения совокупного выпуска является то, насколько быстро наступит долгосрочный период.
При анализе модели IS-LM предполагалось, что уровень цен фиксирован, однако это допущение приемлемо только для краткосрочного периода. Рассмотрим, что происходит с моделью IS-LM в долгосрочном периоде при изменении уровня цен, при этом откажемся от допущения, что номинальные и реальные величины совпадают.
Пусть первоначально экономика находилась в равновесии в точке Е1, в которой фактический объем выпуска равен его естественному уровню (рис. 6.18).
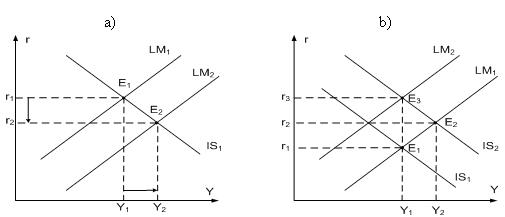
Рис. 6.18. Модель IS-LM в долгосрочном периоде
На рис. 6.18, а рост предложения денег приводит к сдвигу кривой LM вправо в положение LM2 и смещению равновесия в точку Е2, где процентная ставка уменьшается, а совокупный выпуск возрастает до Y2. Так как он превышает естественный объем выпуска, то уровень цен увеличивается, предложение денег в реальном выражении сокращается, а кривая LM вновь сдвигается. Экономика возвращается к начальному равновесию.
На рис. 6.18, b увеличение государственных расходов сдвигает кривую IS в положение IS2, а точка равновесия экономики смещается в положение Е2, в котором ставка возрастает до r2 и совокупный выпуск увеличивается до Y2, что превышает его естественный уровень. Уровень цен начинает расти, а реальные денежные остатки сокращаются, при этом кривая LM сдвигается влево – в положение LM2. Долгосрочное равновесие в точке Е3 устанавливается при еще более высокой процентной ставке, а объем выпуска возвращается к своему естественному уровню.
Таким образом, изучение влияния стимулирующей денежно-кредитной или фискальной политики на модель IS-LM позволяет сделать вывод: денежно-кредитная и фискальная политика могут влиять на совокупный выпуск в краткосрочном периоде, но ни одна из них не влияет на объем выпуска в долгосрочном периоде. Важным моментом при оценке эффективности этих политик с точки зрения увеличения совокупного выпуска является то, насколько быстро наступит долгосрочный период.
§
Экономическая политика государства имеет целью регулирование макроэкономической динамики. Среди моделей, объясняющих причины деловых циклов, – традиционная кейнсианская модель IS-LМ Хикса-Хансена, модель неверных представлений работников, неокейнсианские теории жесткой заработной платы и жестких цен, неокейнсианская модель провалов координации, теория реального делового цикла. Каждая из них по-своему объясняет причины цикличности и по-разному формулирует рецепты проведения экономической политики. Представители каждой теории отстаивают свою точку зрения, дискуссии между ними продолжаются и по сей день, что зачастую служит толчком для дальнейшего развития макроэкономических исследований. Одна из примиряющих позиций состоит в том, что разные рецессии, возможно, имеют различные причины, поэтому для объяснения конкретного рецессионного эпизода можно выбрать наиболее подходящую из перечисленных теорий. Эти подходы кратко описаны в обобщающей таблице 5.1.
Таблица 5.1 – Теоретические взгляды на природу экономических циклов и политику по их преодолению
| Теория | Причины рецессии | Ожидания | Рекомендации по про ведению экономической политики |
| Традиционная кейнсианская модель | Жесткость цен и заработной платы препятствует достижению равновесия при полной занятости | Адаптивные | Проведение стимулирующей монетарной или фискальной политики |
| Модель неверных представлений работников | Ожидаемое снижение реальной заработной платы, вызываемое ожиданием снижения денежной массы, приводит к сокращению предложения труда, уменьшается занятость и выпуск | Рациональные | Только неожиданные изменения предложения денег могут повлиять на занятое п. и выпуск |
| Неокейнсианские теории жесткости заработной платы и цен | Жесткость номинальной зарплаты и цен, долгосрочные контракты, несовершенная информация, издержки меню препятствуют достижению равновесия при полной занятости | Рациональные | В зависимости от причины жесткости номинальных показателей как ожидаемые, так и неожиданные изменения предложения денег могут привести к изменению дохода |
| Неокейнсианская модель провалов координации | Невозможность для фирм вести скоординированную политику приводит к равновесию при низком уровне выпуска (неэффективному по Парето) | Рациональные | Вмешательство правительства может помочь частному сектору выбрать равновесие при высоком выпуске (эффективное по Парето) |
| Теория реального делового цикла | Добровольное снижение работниками предложения труда в периоды низкой заработной платы, являющейся следствием негативных технологических сдвигов | Рациональные | Так как безработица носит добровольный характер, проведение экономической политики нерационально |
Ни одна из перечисленных теорий не способна объяснить все существующие эпизоды рецессии. К тому же иногда очень трудно проинтерпретировать конкретный эпизод с позиций одной теории, поэтому нет единого мнения и относительно путей ее преодоления. Это порождает непрекращающиеся дискуссии об эффективности осуществления макроэкономической политики. Обсуждаются две основные проблемы:
1) Какой должна быть экономическая политика – активной или пассивной?
2) Должна ли экономическая политика следовать заранее оговоренным правилам или проводиться в соответствии с возникшими обстоятельствами?
Часть экономистов (неокейнсианцы) считает, что государство должно проводить кредитно-денежную и бюджетно-налоговую политику, направленную на сглаживание экономических колебаний. Так, во время рецессий следует осуществлять стимулирующую экономическую политику, а во время бумов – ограничительную. Это поможет избежать снижения эффективности функционирования экономики, связанного с недоиспользованием или чрезмерным использованием имеющихся ресурсов.
Экономисты неоклассического направления думают иначе. По их мнению, рыночная экономика является внутренне стабильной и саморегулирующейся системой. Экономические колебания возникают вследствие неудачного вмешательства государства в ее функционирование. Лица, принимающие решения, должны сознавап ограниченность возможностей стабилизационной политики и учитывать вероятные негативные последствия ее проведения.
Таким образом, первые являются сторонниками активной экономической политики, вторые сомневаются в ее эффективности и считают, что она должна быть пассивной.
В качестве критики активного подхода обычно выдвигают следующие аргументы.
1) Сравнительные издержки инфляции и безработицы
Важным моментом является вопрос об издержках проведение стабилизационной макроэкономической политики. Согласно теоретическим представлениям, вытекающим из кривой Филлипса, эта политика приводит к повышению темпов инфляции. Поэтому встает вопрос о сравнительных издержках безработицы и инфляции.
Выигрыш от сокращения безработицы может быть переоценен, так как трудно оценить потенциальный ВВП и, следовательно, измерить разрыв между ним и реальным ВВП. Поэтому ж всегда ясно, когда безработица добровольная, а когда – вынул денная.
С другой стороны, издержки инфляции могут быть недооценены, так как трудно оценить издержки, связанные с неопределенностью темпов инфляции, в результате которой агенты отказываются от принятия решений.
В то же время выигрыш от борьбы с безработицей может быть большим, но временным (пока выпуск не достиг потенциального уровня). Издержки от возникающей при этом инфляции могут быть в каждом периоде незначительными, но суммарный их эффект оказывается существенным, так как в новом долгосрочном равновесии темпы инфляции будут постоянно выше прежнего уровня. Поэтому при принятии решений о проведении стабилизационной политики надо сопоставлять приведенные издержки инфляции с текущим выигрышем от снижения уровня безработицы.
2) Достигает ли активная политика поставленных целей?
Практика показывает, что активное использование бюджетно-налоговой и кредитно-денежной политики сталкивается с большими трудностями из-за существования лагов в ее проведении.
Под лагом экономической политики понимается время, которое проходит между моментом осознания необходимости проведения этой политики и моментом, когда она дает конкретный результат. Обычно считают, что этот лаг является суммой внутреннего и внешнего.
Внутренний лаг представляет собой время, которое проходит с момента осознания потребности в экономической политике до момента начала ее осуществления.
Внешний лаг – время, которое проходит с момента начала осуществления экономической политики до момента, когда она приносит результаты.
С точки зрения внутреннего лага денежная политика имеет несомненные преимущества. Проведение этой политики требует только решения Центрального банка. Изменение бюджетноналоговой политики может занять несколько месяцев, поскольку требуется решение правительства и его утверждение законодательными органами, после чего указ подписывает президент.
С точки зрения внешнего лага, с одной стороны, преимущество имеет бюджетно-налоговая политика, так как она влияет непосредственно на производство. Кредитно-денежная политика обладает большими внешними лагами. Ее воздействие на экономику опосредованное, оно связано с изменением процентных ставок, которые, в свою очередь, влияют на инвестиционные решения. Однако эти решения пересматриваются не сразу, так как планируются заранее. Поэтому результатов кредитно-денежной политики можно ждать довольно долго.
С другой стороны, как было показано ранее, сравнительная эффективность бюджетно-налоговой и кредитно-денежной политики зависит от соответствующих мультипликаторов. Поэтому выбор конкретной формы политики очень сложен, поскольку при ее проведении следует учитывать как лаги, так и мультипликаторы.
Из-за перечисленных проблем экономическая политика может быть применена, когда тенденции уже поменялись. Другими словами, политика против спада может начаться в момент, когда экономика уже вышла из рецессии. Тогда она будет чрезмерно стимулироваться. И наоборот, ограничительная политика начнет оказывать воздействие на экономику после прохождения пика подъема. Тогда ее следствием может оказаться усиление спада.
Сторонники пассивной экономической политики указывают на существование автоматических стабилизаторов, которые по зволяют стимулировать или ограничивать рост ВВП без примения специальных управляющих мер. В качестве таких стабилизаторов обычно рассматривают системы подоходных налогов и социального страхования.
Действительно, объем собираемых подоходных налогов возрастает в период подъема и оказывает, таким образом, ограничительное воздействие на совокупный спрос, что сдерживает чрезмерный рост ВВП. Аналогично сокращение во время спада объема собираемых налогов автоматически оказывает стимулирующее воздействие на экономику и препятствует развитию рецессии.
Во время рецессии объем страховых выплат по безработице увеличивается, что автоматически стимулирует экономику. В период бума снижение этих выплат ограничивает совокупный спрос. Это приводит к сглаживанию циклического подъема.
Действие автоматических стабилизаторов, по мнению сторон ников пассивной политики, обеспечивает быстрое восстановление равновесия без дополнительного вмешательства государства.
3) Несовершенная информация о состоянии экономики
С проблемой существования лагов тесно связана проблема несовершенства информации о текущем состоянии экономики и результатах проводимой экономической политики.
На продолжительность внутренних лагов влияет, в частности, то, что агрегированные данные собираются достаточно редко. Поэтому для принятия решений о проведении экономическом политики используются так называемые опережающие показатели. Речь идет об индикаторах, предупреждающих о наступлении очередной фазы экономического цикла. В качестве примера можно назвать величину запасов, цены на акции, объем заказом, реальные запасы денежных средств, объем кредитов и др. Зачастую изменение этих показателей вызывает необходимость формирования соответствующих мер экономической политики до поступления отчетных агрегированных данных о состоянии экономики. Таким образом управляющие органы стараются снизить продолжительность внутреннего лага. Тем не менее оценка эффективности экономической политики затруднена из-за того, что продолжительность внутреннего и внешнего лага в точности неизвестна. Кроме того, существует неопределенность в оценке результатов политики, во-первых, из-за неточного знания величины мультипликатора; во-вторых, из-за неточного знания реакции экономических агентов на проводимую политику. Так, например, политика снижения налогов, направленная на стимулирование потребления и тем самым совокупного спроса, может привести к увеличению сбережений, в то время как потребление останется неизменным. Реакция экономических агентов на снижение налогов зависит от способа формирования ожиданий и временного горизонта, на котором принимаются решения (см. равенство Рикардо).
4) Рациональность ожиданий и критика Лукаса
Зависимость последствий экономической политики от способа формирования ожиданий породила так называемую критику Лукаса. Суть критики Лукаса заключается в необходимости учета при проведении экономической политики не только текущих ожиданий, но и обратного влияния на ее результаты изменений этих ожиданий (петля обратной связи). Положительный пример критики Лукаса – соотношение потерь и результата при адаптивных и рациональных инфляционных ожиданиях. Традиционное соотношение потерь и результата при проведении ограничительной кредитно-денежной политики может быть существенно снижено и даже сведено к нулю, если экономические агенты формируют свои ожидания рационально.
Пример отрицательного влияния ожиданий на экономическое развитие – история введения инвестиционного налогового кредита для стимулирования совокупного спроса во время рецессий. Фирмы знают, что обычно при спаде правительство вводит инвестиционный налоговый кредит, поэтому при появлении признаков рецессии они приостанавливают инвестиции, ожидая налоговых льгот. В результате инвестиционный спрос падает, что усугубляет рецессию.
Ожидания оказывают существенное влияние на экономическое поведение. К тому же их очень трудно измерить и точно определить, как они изменятся под воздействием экономической политики. Это обстоятельство также затрудняет проведение активной экономической политики.
§
По мере того как общество постепенно осознавало роль принимаемых правительствами решений в области экономической политики, возник вопрос о том, как следует действовать политикам. Поисками ответа на него занимается специальная область экономической теории – нормативная теория экономической политики. Она пытается найти ответы на вопрос, насколько активно правительства должны вмешиваться в экономическую жизнь, не лучше ли экономику в максимальной степени предоставить самой себе? Если вмешательство в экономическую жизнь необходимо, то какие методы регулирования экономики наиболее эффективны?
Другое направление экономической теории занимается анализом практики экономической политики и называется позитивная теория экономической политики.
Специалисты в этой области пытаются найти ответы на вопрос, почему, под давлением каких обстоятельств политики принимают определенные решения, проводят сравнительный анализ практики экономической политики в различных странах.
В данном разделе в основном будет рассматриваться нормативная теория экономической политики, которая была впервые комплексно проанализирована в начале 50-х годов ХХ века голландским экономистом Яном Тинбергеном, ставшим в 1969 году первым лауреатом Нобелевской премии по экономике. Тинберген впервые предложил комплексный анализ теории экономической политики, выявив основные этапы выработки наилучшей (оптимальной) экономической политики.
Прежде всего, правительство должно определить конечные целиэкономической политики. Под конечными целями понимается максимизация общественного благосостояния, интерпретируемого в том или ином виде. Далее правительство должно определить целевые показатели. Часто под целевыми показателями понимаются естественный уровень безработицы и нулевая инфляция. В качестве конечного целевого показателя может быть принята определенная величина производства ВВП или валового национального дохода на душу населения.
Цели экономической политики могут согласовываться между собой или оказываться несовместимыми.
Совместимость целей означает, что достижение одной есть условие реализации другой. В частности, непрерывный экономический рост есть необходимое условие снижения безработицы, роста расходов на программы по социальной защите населения, охрану окружающей среды, гуманизацию рабочих мест, развитие системы здравоохранения.
Несовместимость (несходимость) целей означает, что достижение одной связано с отдалением от других целей. Борьба с инфляцией путем сокращения денежной массы сдерживает совокупный спрос, следовательно, затрудняет экономический рост и достижение полной занятости. С другой стороны, односторонняя политика на достижение полной занятости с помощью «дешевых денег» и высокой государственной задолженности с целью стимулировать совокупный спрос провоцирует рост инфляции. Одновременно нарушается внешнеторговый баланс.
Инструментами, которыми располагает правительстводля достижения той или иной цели, являются известные меры воздействия фискального и кредитно-денежного характера. Это так называемые количественные инструменты воздействия на экономику. Но большое значение имеют и качественные инструменты, применение которых оказывает большое воздействие на формирование деловой среды в стране и в конечном итоге на достижение целевых показателей. Примером такого рода инструментов могут быть различные законодательные акты, регулирующие внешнюю торговлю и движение капитала в страну и из нее. Другой пример – правила, регулирующие процесс создания самостоятельного бизнеса населением: они могут быть простыми и, тем самым, способствовать развитию экономической активности населения и, как следствие, росту производства и занятости или забюрократизированными, что будет препятствовать развитию бизнеса и росту ВВП. В дальнейшем в анализе речь будет идти о количественных инструментах.
Конечные цели и инструменты экономической политики должны быть согласованы, увязаны между собой. Такого рода согласование проводится с использованием различных моделей экономической политики.
После того как с использованием моделей экономической политики определены набор и параметры инструментов, на практике правительству необходимо организовать процесс достижения необходимых целей.
Для анализа экономической политики Тинберген использовал простую линейную модель. Экономическая логика этой модели строилась по следующей схеме: в качестве исходной точки в формировании экономической политики берется минимально возможное количество взаимозависимых целевых показателей. В модели экономической политики Тинбергена рассматривается два целевых показателя и два инструмента макроэкономической политики. Пусть T1 и T2 – два целевых показателя, I1 и I2 – два инструмента экономической политики. Желаемый уровень целевых показателей обозначим как T1* и T2*. Если экономика находится в состоянии, когда достигнуты оба целевых показателя, то принято говорить, что она находится в точке оптимума (т.н. «точка блаженства» по Тинбергену).
Связь между целевыми показатели и инструментами описывается с помощью простой линейной модели.
T1 = a1∙I1 a2∙I2, (1.1)
T2 = b1∙I1 b2∙I2. (1.2)
Экономическая политика может достигнуть обеих целей только тогда, когда влияние инструментов на цель линейно независимо друг от друга. Математически это условие достигается, если имеет место следующее неравенство: a1/b1 ≠ a2/b2. Если же имеет место равенство a1/b1 = a2/b2, то возможно достижение лишь одной из поставленных целей, что доказывается следующим образом.
Пусть имеет место равенство a1/b1 = a2/b2. Тогда после простых преобразований можно получить следующее равенство: b2/b1 = a2/a1. Если разделить правую и левую часть соотношения (1.1) на a1 и правую и левую часть соотношения (1.2) на b1, они могут переписаны в следующем виде:
T1/a1 = I1 a2/a1∙I2, (1.3)
T2/b1= I1 b2/b1∙I2. (1.4)
С учетом равенства b2/b1 = a2/a1 уравнение (1.4) может записано следующим образом:
T2/b1 = I1 b2/b1∙I2 = I1 a2/a1∙I2 = T1/a1. (1.5)
Аналогичную подстановку можно сделать и в уравнение (1.3). Из уравнения (1.5) следует, что, если описанная им комбинация инструментов экономической политики будет использована a1 раз, то будет достигнута цель T1. Если эта же комбинация будет использована b1 раз, то будет достигнута цель T2. Однако невозможно достичь обеих целей одновременно.
Запишем теперь математическое выражение, позволяющее определить значение инструментов при достижении точки оптимума:
T1* = a1∙I1 a2∙I2, (1.6)
T2* = b1∙I1 b2∙I2. (1.7)
После преобразований получим следующие значения для инструментов экономической политики.
I1 = (b2∙T1* – a2∙T2*)/(a1∙b2 – b1∙a2), (1.8)
I2 = (a1∙T2* – b1∙T1*)/(a1∙b2 – b1∙a2). (1.9)
Таким образом, при линейной независимости инструментов экономика достигнет точки оптимума в случае, если они будут иметь значения, определяемые уравнениями (1.8) и (1.9).
Обобщение полученного вывода состоит в следующем. В экономике, которая может быть описана системой линейных уравнений с n целевыми показателями, данные показатели могут быть достигнуты при наличии n линейно независимых инструментов экономической политики.
Рассмотрим конкретный пример для системы уравнений (1.1)-(1.2). Пусть целевыми показателями являются ВВП при безработице, находящейся на естественном уровне (Y = Y*), и нулевая инфляция (π = π*). В качестве инструментов рассмотрим изменение денежной массы M и государственных затрат G. Тогда связь между целевыми показателями и инструментами экономической политики описывается следующими уравнениями.
Y = a1∙G a2∙M, (1.10)
π = b1 ∙G b2∙M. (1.11)
В этом случае коэффициенты a и b характеризуют следующие параметры:
—a1 и b1 –количественные эффекты влияния фискальной политики на выпуск и инфляцию;
—a2 и b2 – количественные эффекты влияния денежной политики на выпуск и инфляцию.
Эти числовые значения получают из различных макроэкономической моделей, в частности, модели IS-LM.
Данные соотношения показывают:
—b1/a1 – насколько повышается инфляция, если в результате фискальной политики выпуск возрастает на единицу;
—a1/b1 – насколько возрастет выпуск, если в результате фискальной политики инфляция возрастает на единицу;
—b2/а2 – насколько увеличивается инфляция, если количество денег увеличивается таким образом, что выпуск возрастает на единицу;
—a2/b2 – насколько возрастает выпуск, если в результате денежной политики инфляция возрастает на единицу.
Из экономической теории известно, что денежная масса и фискальные рычаги как инструменты экономической политики оказывают влияние на каждую цель. Отсюда Тинберген сделал фундаментальный вывод, что экономическая политика может достичь обеих целей тогда, когда она имеет в своем распоряжении оба инструмента, и влияния инструментов на цель линейно независимы друг от друга.
Пусть экономика находится в состоянии, когда инфляция π = 4% в год, а ВВП равен его значению при естественном уровне безработицы (Y = Y*). Цели правительства состоят в удержании ВВП на достигнутом уровне при снижении инфляции до нуля. Таким образом, цели политики состоят в том, чтобы Δπ = -4%, ΔY = 0. Перепишем систему уравнений (1.10)-(1.11) в терминах приростов с учетом требуемых численных значений изменения целевых показателей.
0 = a1∙G a2∙M, (1.12)
-4 = b1 ∙G b2∙M. (1.13)
После проведения простых преобразований получим следующие значения целевых показателей.
ΔG = 4∙a2/(a1∙b2 – b1∙a2), (1.14)
ΔM = -4∙a1/(a1∙b2 – b1∙a2). (1.15)
Необходимо помнить, что рассматриваемая модель Тинбергена является очень сильным упрощением действительности. На практике, при определенном сочетании численных значений коэффициентов a1, a2, b1, b2 расчетная величина изменения инструментов может быть такой, что, например, требуемая вариация ΔG может привести к недопустимому дефициту государственного бюджета или существенное изменение ΔM через определенное время породит большую инфляцию. Такого рода проблемы возникают в случае, когда a1/ b1 и a2/ b2 не равны, но имеют весьма близкие значения. В этом случае знаменатель в уравнениях (1.8) и (1.9) весьма близок к нулю и ΔI1, ΔI2 могут иметь очень значительные, недопустимые для практического применения значения.
§
Иная интерпретация проблемы выбора экономической политики была предложена Робертом Манделлом. Исходя из наблюдений за реальной экономической политикой он предположил, что различные инструменты экономической политики находятся под контролем различных органов государственного управления. Например, монетарная политика находится под контролем Центрального банка, а фискальная – под контролем правительства страны. Органы управления в модели Манделла действуют не скоординированным образом, т.е. децентрализовано. Р. Манделл показал, что если инструменты экономической политики правильно «приписаны» к органам управления, то оптимальное значение целей экономической политики может быть достигнуто в условиях, когда решения принимаются децентрализовано. Концепция эффективной рыночной классификации, предложенная Р. Манделлом, исходит из того, что каждая цель экономической политики должна быть «приписана» к тому инструменту (и, соответственно, к органу государственного управления), который оказывает на нее большее воздействие и имеет преимущество перед другими мерами воздействия на данный показатель с точки зрения его регулирования.
Например, изменение денежной массы M, осуществляемое центральным банком, оказывает большее воздействие на изменение инфляции π по сравнению с инструментом фискальной политики G. Математически это означает, что в системе уравнений (1.10)-(1.11) отношение и b2/a2 больше, чем отношение b1/a1. Следовательно, органы, отвечающие за кредитно-денежную политику (прежде всего, Центральный банк) должны управлять инфляционными процессами, а органы, под контролем которых находится фискальная политика, отвечают за изменение динамики ВВП. В случае такого распределения обязанностей между органами управления государством инструменты M и G будут стремиться к своему оптимальному значению. Наоборот, при попытке правительства регулировать инфляцию, а центрального банка – динамику ВВП, невозможно получить процесс, сходящийся к оптимальным значениям инструментов экономической политики.
В упрощенном варианте модели Тинбергена был рассмотрен случай, когда есть две цели и два инструмента. В реальной жизни встречаются ситуации, когда инструментов, которыми располагают органы управления экономикой, меньше, чем целевых показателей. В этом случае невозможно достижение оптимальных значений всех показателей и возникает проблема минимизации потерь, связанных с не оптимальностью значений инструментов.
Представим ситуацию, когда использование государственных затрат как инструмента макроэкономического регулирования на какой-то период времени невозможно. Например, это может быть в случае, когда дальнейший их рост приведет к недопустимому дефициту государственного бюджета. Следовательно, изменение государственных затрат должно быть нулевым (ΔG = 0). В терминах модели (1.10)-(1.11) это означает, что существует лишь один реальный инструмент воздействия на экономическую систему – изменение денежной массы. С учетом того, что ΔG = 0, уравнения (1.10)-(1.11) в терминах приростов могут быть записаны следующим образом:
ΔY = a2∙ΔM, (1.16)
Δπ = b2∙ΔM. (1.17)
Из (1.16) следует, что ΔM = ΔY/a2. Подставив это значение ΔM в уравнение (1.17), получим следующее соотношение:
Δπ = (b2/a2)∙ΔY. (1.18)
Из соотношения (1.18) следует, что при неизменных a2 и b2 невозможно уменьшить инфляцию без сокращения ВВП.
Как уже отмечалось выше, в условиях меньшего по сравнению с целями числа инструментов перед правительством встает вопрос о минимизации обществом потерь, связанных с тем, что целевые показатели не достигнут своих оптимальных значений. В связи с этим в анализ вводится функция социальных потерь, которая может быть сформулирована следующим образом.
L2 = (ΔY – ΔY*)2 (Δπ – Δπ*)2, (1.19)
где ΔY*, Δπ* – оптимальные значения изменения ВВП и инфляции.
Возведение в квадрат разницы между фактическим и оптимальным значением изменения целевых показателей является стандартным приемом, позволяющим избежать взаимного «поглощения» отклонений с различными знаками. Например, может иметь место ситуация, когда (ΔY – ΔY*) < 0, а (Δπ – Δπ*) > 0 и сумма этих показателей может быть существенно ниже, чем каждое слагаемое в отдельности.
В более общем виде функция социальных потерь может быть описана следующим образом.
L2 = (ΔY – ΔY*)2 α∙(Δπ – Δπ*)2, (1.20)
где α > 0 – весовой коэффициент, который показывает, достижение какой цели является более приоритетным для правительства. Например, при α > 1 более важным является достижение цели по снижению инфляции. При α < 1 – более приоритетна цель по изменению ВВП.
Для приведенного выше примера (уравнения (1.10)-(1.13)) функция социальных потерь будет иметь следующий вид.
L2 = (ΔY)2 α∙(Δπ 4)2. (1.21)
При предположении о том, что α = 1, уравнение (1.21) будет иметь вид.
L2 = (ΔY)2 (Δπ 4)2. (1.22)
Точкой оптимума, в которой социальные потери равны нулю, будет точка с координатами ΔY = 0 и Δπ = -4.
Дадим геометрическую интерпретацию функции социальных потерь. Кривая безразличия функции социальных потерь L2 представляет собой окружность (кривую безразличия) радиуса L с центром в точке оптимума A с координатами (-4;0) (рис. 5.1). В случае бóльших потерь кривая безразличия представляет собой бóльшую окружность c тем же центром и с бóльшим радиусом.
Рисунок 5.1 – Функция социальных потерь в системе координат (Δπ, ΔY)
Линия T на рис. 5.1 представляет собой графическое изображение функции, описываемой уравнением (1.18). Она показывает то реальное ограничение, с которым сталкивается правительство при реализации своих попыток снизить инфляцию. Так как идеальной точкой для органов управления экономикой является точка оптимума А, целью правительства является максимальное приближение к ней. Очевидно, что такое максимальное приближение будет иметь место в точке касания кривой безразличия L02 и линии T. На рис. 4 это точка B, которую можно получить как перпендикуляр их точки А. В данном примере L02 является ближайшей к точке оптимума А кривой безразличия, касающейся линии Т.
Кривые социальных потерь и прямая возможных значений инфляции и выпуска (линия Т) позволяют найти такую точку соотношения инфляции и выпуска, при которых общество понесет наименьшие потери. В точке B достигается такой компромисс. Инфляция заметно снижается, хотя и не на желаемую оптимальную величину. Одновременно на некоторую величину -ΔYB уменьшается ВВП, что является своеобразной «платой» общества за уменьшение темпов роста цен. В случае достижения нулевой инфляции эта плата была бы слишком велика, так как ВВП снизился бы на значительно большую величину -ΔYA.
§
В проведенных выше рассуждениях о выборе наилучшей экономической политики мы абстрагировались от фактора неопределенности. В действительности органы управления экономикой имеют дело со стохастической системой и не могут точно оценить последствия принимаемых ими решений. В частности, если оценить с помощью методов математической статистики значения коэффициентов a1, a2, b1, b2 в уравнениях (1.10)-(1.11), имея данные о динамических рядах показателей этих уравнений в ретроспективе, это не означает, что в будущем эти коэффициенты будут иметь такие же значения. Также большую роль во влиянии инструментов экономической политики на динамику целевых показателей имеют временные лаги (см. выше). Например, увеличение государственных затрат окажет влияние на темп роста ВВП лишь через определенной время. При этом значение этого временного интервала также является стохастической величиной. Наконец, на экономическую систему воздействуют различного рода экзогенные факторы: природные катаклизмы (засухи, наводнения, землетрясения и т. д.), войны, терроризм и др.
Простейшая модель экономики с одним целевым показателем ΔY* > 0 и с использованием одного инструмента экономической политики ΔMс учетом неопределенности может быть записана следующим образом:
ΔY = φ*ΔM ε, (1.23)
где ε – случайная величина, отражающая воздействие на ΔY прочих не учтенных в явном виде факторов.
Так как эффект влияния на ΔY величины ε суммируется с эффектом влияния изменения денежной массы, такого рода случайные величины характеризуют аддитивную неопределенность. Коэффициент φ также является случайной величиной. Поэтому невозможно точно спрогнозировать влияние изменения денежной массы на динамику ВВП. Но в отличие от ε коэффициент φ умножается на величину изменения денежной массы и принято говорить, что такого рода случайные величины отражают влияние мультипликативной неопределенности.
Одна из возможностей для органов управления экономикой состоит в применении для оценки последствий использования инструментов экономической политики средних значений случайных величин ε и φ. Однако в действительности они могут оказаться ниже своих средних значений и ожидаемое изменение ВВП не будет достигнуто или станет выше средних значений и ВВП изменится больше, чем это планировалось. Например, темп роста продукта будет выше прогнозного и произойдет «перегрев» экономики, что в будущем чревато негативными последствиями.
Величина φ умножается на изменение инструментов экономической политики. Поэтому влияние мультипликативной неопределенности на достижение конечных целей экономической политики намного сильнее, чем влияние аддитивной неопределенности.
Исследования показали, что при принятии решений органы управления могут ориентироваться на средние значения случайной величины ε, характеризующей аддитивную неопределенность. Однако со случайной величиной φ следует быть намного осторожней. Ее значение при оценке последствий влияния инструментов экономической политики в будущем следует принимать ниже среднего [2].
| 2.2. Экономическая политика в условиях неопределенности |
| В реальной практике правительства сталкиваются с ситуацией, когда неясно, какое влияние окажут их действия на целевые показатели. Существует несколько видов неопределенности. 1. Неопределенность числовых коэффициентов. Числовые коэффициенты a и b имеют средние значения, на их значение действует временной фактор, они рассчитываются на основе прошлых данных, а применяются для оценки политики в будущем. 2. Неопределенность существует также в том, что, зная, что изменения должны произойти, неясно, когда и как это произойдет. Поэтому консерватизм экономической политики является фактором, снижающим риски от неопределенности числовых коэффициентов. Если изменения не происходят, не следует слишком часто менять инструменты. 3. На целевые показатели воздействуют экзогенные переменные (экзогенные шоки), которые невозможно предусмотреть. Рассмотрим влияние фактора неопределенности на экономическую политику. Возьмем только один показатель Y(выпуск)и один инструмент DМ (денежная политика). Тогда зависимость выпуска и инструмента будет иметь вид: DY = aDМ. Предположим, что национальная экономика находится на стадии конъюнктурного спада. Поэтому главной целью экономической политики является увеличение выпуска: DYl>0. Введем в расчеты элемент неопределенности e.Тогда формула расчета будет иметь следующий вид: DY = 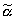 DМ DМ 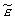 . .Значение 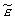 в данном соотношении может отражать влияние таких экзогенных переменных, как: в данном соотношении может отражать влияние таких экзогенных переменных, как:· забастовки, которые влияют на выпуск, но находятся вне контроля правительства; · погода, снижающая объемы выпуска в отраслях первичного сектора экономики. Переменные 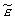 и и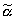 –величины случайные. –величины случайные.Поскольку числовое значение коэффициентов точно определить нельзя, то они пишутся со значком “тильда” (~). Значение 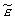 может быть и положительным, и отрицательным, со средним значением, равным нулю. Такой тип ошибок называется аддативной неопределенностью. Поэтому ее эффект суммируется с эффектами влияния политических инструментов. может быть и положительным, и отрицательным, со средним значением, равным нулю. Такой тип ошибок называется аддативной неопределенностью. Поэтому ее эффект суммируется с эффектами влияния политических инструментов.При выборе инструмента экономической политики известно лишь среднее значение 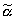 , но не известен его точный числовой параметр. Поэтому невозможно точно предсказать влияние денежной политики на выпуск. Говоря формально, коэффициент , но не известен его точный числовой параметр. Поэтому невозможно точно предсказать влияние денежной политики на выпуск. Говоря формально, коэффициент 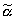 вносит мультипликационную неопределенность, поэтому он умножается на эффект влияния инструмента, в данном случае денежной политики. вносит мультипликационную неопределенность, поэтому он умножается на эффект влияния инструмента, в данном случае денежной политики.К чему приводит наличие неопределенности? Достижение целевых показателей возможно как тенденция, то есть в среднем: DY= 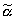 DМ DМ 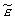 . .Таким образом: DМ=  . .Поскольку DМ зависит, в основном, от значений коэффициента 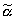 , то если он будет ниже среднего значения, тогда денежная политика будет слабой и уровень выпуска тоже окажется ниже ожидаемого. Если значение коэффициента будет выше среднего, то выпуск окажется выше. Это приведет к сверхзанятости и возникнет дефицит спроса. , то если он будет ниже среднего значения, тогда денежная политика будет слабой и уровень выпуска тоже окажется ниже ожидаемого. Если значение коэффициента будет выше среднего, то выпуск окажется выше. Это приведет к сверхзанятости и возникнет дефицит спроса.Коэффициент 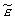 не оказывает влияния на выбор денежной политики. не оказывает влияния на выбор денежной политики. |
§
В середине 1970-х гг. профессор Чикагского университета Роберт Лукас подверг серьезной критике теорию экономической политики Тинбергена и поставил под сомнение саму возможность использования результатов расчетов по укрупненным эконометрическим моделям при принятии решений в области экономической политики [3].
В макроэкономических моделях предполагается, что определенные на основе ретроспективного анализа динамических рядов коэффициенты в уравнениях, описывающих связь между инструментами экономической политики и целевыми показателями, являются стабильными величинами, которые могут быть использованы при прогнозировании.
Р. Лукас оспаривает этот принципиальный тезис. Он говорит, что в условиях отсутствия заметных изменений в экономической политике полученные коэффициенты уравнений связи инструментов экономической политики с целевыми показателями могут достаточно корректно описывать поведение экономики. Однако, при существенном изменении экономической политики значения коэффициентов в эконометрических моделях могут измениться (в нашем случае это значение коэффициентов a1, a2, b1, b2 в уравнениях (1.1), (1.2)). Этот факт может обнаружиться позже во время переоценки коэффициентов модели. Следовательно, политики будут принимать решения, основываясь на результатах расчетов по модели, где количественные взаимосвязи описаны некорректно.
В соответствии с подходом, предлагаемым Р. Лукасом, центральной проблемой является то, как в моделях трактуются ожидания. В эконометрических моделях ожидаемые значения прогнозных показателей формируются на основе функций, построенных на ретроспективной информации. Как уже было отмечено, при резкой смене экономической политики эти функции могут дать недостоверные значения ожидаемых (прогнозных) переменных.
Поясним сказанное на простом примере. С помощью методов математической статистики можно оценить параметры уравнения связи прироста ВВП (Y) и прироста денежной массы (M) в данном периоде относительно предыдущего:
ΔY = b0 b1(M – M–1). (4.27)
В соответствии с подходом, разработанным Тинбергеном, полученные коэффициенты b0, b1 можно использовать для определения влияния прироста денежной массы в будущем на динамику ВВП. Однако, в соответствии с подходом Лукаса модель (17.27) не следует применять для принятия решений в области экономической политики. В соответствии с теорией рациональных ожиданий связь между величиной прироста Y и величиной прироста денежной массы следовало бы оценивать следующим соотношением:
ΔY = g g (M – Me), (4.28)
где Me – ожидавшаяся в предыдущем периоде величина денежной массы текущего периода.
Следовательно, если реальная величина денежной массы в данном периоде будет весьма близка к ожидавшемуся значению, то это не окажет (или почти не окажет) влияния на прирост ВВП. Влияние на ΔY окажет лишь неожиданное отклонение денежной массы от ожидаемой величины.
Б. Функция предложения Роберта Лукаса. Производители сталкиваются с проблемой интерпретации фактического увеличения цены на индивидуальном рынке:
Рынок каждого отдельного товара похож на остров; участники рынка и обитатели острова владеют всей информацией о нем, однако при этом они отделены от других рынков (или островов) и узнают обо всем происходящем за пределами их острова только с опозданием (лагом).
В таких условиях производители сталкиваются с особенно сложной проблемой: когда рыночная цена на их продукцию поднимается, производители не знают наверняка, выросла ли относительная цена на их продукцию (в этом слу-
чае они хотели бы увеличить предложение) или же возросли все цены (в этом случае они не хотели бы увеличить предложение).
Индивид или фирма, действующие в соответствии с рациональными ожиданиями, расценивают произошедшее увеличение цен на локальном рынке частично как повышение общего уровня цен, а частично как увеличение относительной цены товара.
Таким образом, даже если экономика испытывает воздействие общеэкономического шока совокупного спроса, то каждый производитель думает, что относительная цена его товара все же увеличилась на некую величину — такова ошибка восприятия.
В действительности относительные цены не изменились: произошел рост общего уровня цен; тем не менее результат таков, что шок совокупного спроса ведет к сознательному увеличение совокупного предложения экономическими агентами.
Функция предложения Лукаса:
Y = Yh α х (Р — Ре)
Выпуск в любой конкретный период определяется двумя элементами: 1) естественным уровнем выпуска (Yh), соответствующим естественному уровню безработицы; 2) циклическим компонентом, равным разнице между фактическим (Р) и ожидаемым уровнем (Ре) цен. «Ценовый сюрприз»:если Р больше, чем Ре, то каждый индивидуальный производитель считает, что относительные цены его собственного товара выросли, хотя на самом деле изменился лишь общий уровень цен.
Важное следствие модели Лукаса: ожидаемые изменения предложения денег, скорее всего, влияют только на цены, но не на выпуск, если предположить, что все экономические агенты понимают механизмы функционирования экономики и их ожидания рациональны; только неожиданные изменения денежной политики могут повлиять на выпуск; если все экономические агенты понимают, что вот-вот произойдет увеличение денежного предложения, то они наверняка знают то, что все цены увеличиваются в равных пропорциях (т.к. при этом кривая совокупного спроса сдвинется вверх вдоль вертикальной кривой совокупного предложения); при увеличении цен на ожидаемую величину производители не заблуждаются относительно причин такого увеличения и не считают, что произошло изменение относительных цен, а значит совокупное предложение остается неизменным.
Общие положения и выводы из проведенного в данном разделе анализа сводятся к следующему.
1. В теоретическом анализе экономической политики принято выделять два подхода. Первый – нормативная теория экономической политики, которая изучает вопрос о том, насколько активно правительства должны вмешиваться в экономическую жизнь и какие методы регулирования экономики наиболее эффективны. Второй – позитивная теория экономической политики, которая исследует реальную экономическую политику и пытается дать ответ на вопрос, чем были обусловлены конкретные политические решения, проводит сравнительный анализ практики экономической политики в различных странах.
2. Впервые комплексную модель экономической политики предложил голландский экономист Ян Тинберген. С помощью линейной модели он показал, что в случае двух целевых показателей и двух инструментов экономической политики можно достигнуть желаемого значения показателей при условии, когда эффекты влияния инструментов на цели линейно независимы. Обобщением этого результата является то, что в экономике, кото рая описывается системой линейных уравнений с n целевыми показателями, данные показатели могут достигнуть желаемых значений при наличии n линейно независимых инструментов экономической политики.
3. Анализ экономической политики с использованием эффективной рыночной классификации Роберта Манделла исходит из того, что каждая цель может быть «приписана» к определенному инструменту и, соответственно, органу государственного управления, который наиболее значительно влияет на данную цель. В условиях, когда органы государственного управления действуют не скоординированным образом, оптимальный набор политических целей может быть достигнут при условии правильной «приписки» инструментов к целям.
4. В ситуации, когда инструментов экономической политики меньше, чем целей, общество сталкивается с проблемой минимизации потерь от того, что целевые показатели не достигнут желаемого значения. Решение этой проблемы проводится с использованием функции социальных потерь.
5. Органы государственного управления имеют дело с экономикой, которая является стохастической системой. Поэтому при подготовке решений необходимо учитывать фактор неопределенности. В анализе экономической политики принято выделять два типа неопределенности: аддитивную и мультипликативную. Аддитивная неопределенность связана с экзогенными шоками, такими как землетрясения, погодные аномалии и т. д. Она не оказывает существенного влияния на выбор экономической политики, и значения соответствующих переменных при прогнозировании могут быть приняты на уровне их математических ожиданий. Мультипликативная неопределенность усиливает эффект от применения инструментов экономической политики. Поэтому органы управления экономикой при оценке последствий влияния инструментов экономической политики в будущем должны принимать значения параметров, отражающие мультипликативную неопределенность, на уровне ниже математического ожидания.
6. Теория экономической политики была подвергнута критике Робертом Лукасом. Он поставил под сомнение корректность подхода, реализуемого в макроэкономических моделях, в которых не находят должного отражения ожидания. При резкой смене экономической политики полученные с их применением прогнозы могут оказаться недостоверными. Конструктивный вывод из критики Лукаса состоит в необходимости совершенствования макроэкономических моделей в направлении более корректного отражения в них ожиданий. Примером такого конструктивного подхода является учет ожидаемой инфляции при прогнозировании темпа роста цен.
14.1. Политика по правилам или политика ПО ОБСТОЯТЕЛЬСТВАМ?
При обсуждении проблем формирования экономической политики одним из дискуссионных является вопрос о том, должны ли правительственные органы действовать по установленным заранее правилам, определяющим выбор в каждый момент времени, или же такие правила отсутствуют и политики обладают свободой действия исходя из сложившихся обстоятельств в каждый момент времени. Соответственно различают политику «по правилам» (ex-ante) и политику «по обстоятельствам» (ex-post).
Примерами политики по правилам в денежно-кредитной сфере могут служить поддержание постоянных темпов роста денежной массы, поддержание темпов роста номинального выпуска. В качестве правила бюджетно-налоговой политики можно рассматривать требование сбалансированности бюджета, политику сглаживания налогов, поддержания платежеспособности по внутреннему долгу.
Политика по правилам и дискреционная политика может проводиться как в рамках активной, так и в рамках пассивной экономической политики. Так, правило кредитно-денежной политики, состоящее в поддержании постоянных темпов роста денежной массы, является примером пассивной экономической политики. Правило увеличения денежной массы на величину «уровень безработицы минус шесть процентов» — пример активной экономической политики.
Одним из доводов в пользу политики по правилам является существование проблемы динамической непоследовательности в экономической политике.
Правительство может облегчить достижение цели, формируя ожидания. Но в условиях сформировавшихся ожиданий частного сектора для него как для рационального агента часто выгоден отход от провозглашенной ранее политики. Примером непоследовательности монетарной политики может служить возникающий при ее проведении компромиссный выбор между инфляцией и безработицей. Согласно кривой Филлипса взаимосвязь между ними зависит от инфляционных ожиданий. Центральный банк старается сформировать ожидания низкой инфляции. Для этого он заявляет, что главной целью проводимой политики является снижение темпов роста цен. Однако, после того как ожидания уже сложились и основанные на них экономические решения приняты, у него возникает соблазн сократить уровень безработицы ценой некоторой инфляции. Рациональные экономические агенты это понимают и не доверяют объявленным целям снижения инфляции.
В этих условиях выходом является политика по правилам. Если обязать Центральный банк поддерживать постоянный низкий теми инфляции, экономические агенты будут уверены в этой политике и инфляция снизится без повышения уровня безработицы.
Можно привести и примеры динамической непоследовательности бюджетно-налоговой политики:
1) для стимулирования инвестиционной активности правительство объявляет об освобождении доходов на капитал от налогообложения. Но, после того как капитал уже инвестирован, оно оказывается заинтересованным в отказе от своих обещаний, так как налоги на уже функционирующий капитал не подрывают экономических стимулов;
2) правительство обещает сурово наказывать тех, кто уклоняется от уплаты налогов. Однако, после того как уклонение уже произошло и обнаружено, правительство, возможно, прибегнет к налоговой амнистии, благодаря которой виновные смогут избежать тюремного заключения при условии выплаты ими всех налогов.
Таким образом, проведение политики по правилам снимает проблему недоверия к проводимой экономической политике и, следовательно, повышает ее эффективность.
Еще одним аргументом в пользу политики по правилам является возможность оппортунистического поведения лиц, принимающих решения. Они могут, во-первых, быть некомпетентны; во-вторых, преследовать собственные интересы в ущерб общественным; в-третьих, проводить политику, направленную на сохранение политической власти, не заботясь об экономических последствиях.
Стандартными способами преодоления динамической непоследовательности являются политика по правилам и делегирование полномочий по проведению кредитно-денежной политики независимому от правительства Центральному банку.
Зачастую в результате непоследовательной политики правительства возникает кризис доверия к нему со стороны экономических агентов. В условиях, когда правительство не в состоянии повлиять на экономические ожидания, предлагается проводить меры, вынуждающие фирмы и работников вести себя таким образом, как если бы они ожидали низкую инфляцию, создавая издержки повышения цен и заработной платы. Это может быть сделано с помощью замораживания заработной платы и цен либо путем проведения так называемой политики доходов. Последняя основана на взимании дополнительных налогов при повышении зарплаты и цен.
Несмотря на кажущуюся простоту, подобная политика имеет свои отрицательные стороны:
— она препятствует изменению относительных цен, которое обеспечивает достижение равновесия при полной занятости;
— без дополнения другими мерами она может привести к нежелательным последствиям.
Так, например, замораживание темпов роста зарплаты и цен при прежних темпах роста денежной массы ведет к росту реальных запасов денежных средств, что может оказать стимулирующее влияние на совокупный спрос. Поскольку реальная зарплата прежняя, то выпуск и занятость не изменяются. В результате возникает дефицит на рынке товаров и услуг, следствием которого является подавленная инфляция. Продолжение в этих условиях политики контроля цен и заработной платы приведет в конце концов к резкому росту цен.
Означает ли все предыдущее, что не надо проводить экономическую политику? Вся послевоенная экономическая история свидетельствует в пользу ее проведения, так как послевоенные рецессии были короче и менее болезненны, чем довоенные. Противники активной экономической политики утверждают, что это не так, поскольку после войны улучшилось качество экономических данных. Поэтому вывод о длительности и глубине довоенных рецессий ошибочен, так как основан на некачественной экономической информации. Однако изменение качества данных не может отменить самого факта существования рецессий. Одновременно невозможно отрицать, что стабилизационная политика дала положительные результаты.
Многие тем не менее утверждают, что, если исключить из рассмотрения Великую депрессию, развитие не стало более стабильным после Второй мировой войны, и высказывают скептицизм по поводу возможностей стабилизации экономики с помощью экономической политики.
Однако сам факт проведения такой политики во всех странах свидетельствует в пользу ее эффективности. В противном случае следует считать, что все современные правительства заблуждаются или проводят оппортунистическую политику.
Тем не менее проблемы проведения экономической политики остаются дискуссионными и споры продолжаются и по сей день.
Оптимальный уровень нормы сбережений (золотое правило)
После нахождения устойчивого уровня k∗{displaystyle k^{*}} следующей задачей является нахождение такого значения нормы сбережений s∗{displaystyle s^{*}}, при котором в устойчивом состоянии потребление на единицу эффективного труда c{displaystyle c} максимально. То есть, необходимо решить задачу[18][19]:
- maxsc[k(s)]{displaystyle max _{s}{c[k(s)]}}
при условии:
- k˙=0{displaystyle {dot {k}}=0}.
Выразив c{displaystyle c} через k{displaystyle k}, получим[20]:
- c[k(s)]=(1−s)y=f[k(s)]−(n g δ)k(s){displaystyle c[k(s)]=(1-s)y=f[k(s)]-(n g delta )k(s)}.
Производная ∂c∂s{displaystyle {frac {partial c}{partial s}}} равна[20]:
- ∂c∂s=(∂f∂k−(n g δ))∂k∂s{displaystyle {frac {partial c}{partial s}}={biggl (}{frac {partial f}{partial k}}-(n g delta ){biggr )}{frac {partial k}{partial s}}}.
В точке максимума ∂c∂s=0{displaystyle {frac {partial c}{partial s}}=0}. С ростом нормы сбережений капиталовооружённость на единицу эффективного труда растет, потому ∂k∂s>0{displaystyle {frac {partial k}{partial s}}>0}. Значит, в точке максимума должно выполняться равенство[20]:
- ∂f(k∗∗)∂k=n g δ{displaystyle {frac {partial f(k^{**})}{partial k}}=n g delta },
где k∗∗{displaystyle k^{**}} — устойчивый уровень капиталовооружённости на единицу эффективного труда, соответствующий максимальному потреблению.
Таким образом, норма сбережений s∗{displaystyle s^{*}}, максимизирующая потребление c{displaystyle c}, находится из решения системы уравнений[20]:
- {s∗f(k∗∗)=(n g δ)k∗∗,∂f(k∗∗)∂k=n g δ.{displaystyle {begin{cases}s^{*}f(k^{**})=(n g delta )k^{**},\{frac {partial f(k^{**})}{partial k}}=n g delta .end{cases}}}
В результате решения этой системы оптимальная норма сбережения, соответствующие «Золотому правилу», равна эластичности выпуска по капиталу[21]:
- s∗=k∗∗f(k∗∗)×∂f(k∗∗)∂k{displaystyle s^{*}={frac {k^{**}}{f(k^{**})}}times {frac {partial f(k^{**})}{partial k}}}.
Графически «Золотое правило» нормы сбережения в модели Солоу показано на иллюстрации. Выбирается такая норма сбережений, при которой наклон кривой f(k){displaystyle f(k)} равен n g δ{displaystyle n g delta }, поскольку именно в этой точке превышение кривой f(k){displaystyle f(k)} над кривой (n g δ)k{displaystyle (n g delta )k}, которое и составляет потребление c{displaystyle c}, максимально. Таким образом, норма сбережений, обеспечивающая максимальный устойчивый уровень потребления, равна эластичности выпуска по капиталу в устойчивом состоянии, соответствующему этой норме сбережений. Полученное значение s∗{displaystyle s^{*}} называют «Золотым правилом» нормы сбережения, а k∗∗{displaystyle k^{**}} — капиталовооружённостью на единицу эффективного труда, соответствующей «Золотому правилу»[21].
Если норма сбережений s{displaystyle s} выше «Золотого правила», то при её снижении до уровня «Золотого правила» потребление c{displaystyle c} сначала резко растет, затем снижается, но в итоге стабилизируется на уровне выше исходного[22]. Изменение показателей с течением времени при таком переходе к «Золотому правилу» представлено на иллюстрации вариант 1.
Если норма сбережений s{displaystyle s} ниже «Золотого правила», то при её росте до уровня «Золотого правила» потребление c{displaystyle c} сначала снижается, но затем растет и превышает исходный уровень[21]. Изменение показателей с течением времени при таком переходе к «Золотому правилу» представлено на иллюстрации вариант 2.
Если в качестве производственной функции в модели используется функция Кобба-ДугласаY(K,LE)=Kα(LE)1−α{displaystyle Y(K,LE)=K^{alpha }(LE)^{1-alpha }}, у которой эластичность выпуска по капиталу постоянна, то s∗=α{displaystyle s^{*}=alpha }[21].


































![{displaystyle max _{s}{c[k(s)]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86b50f47cd2f8088d3fd1443adad41e65fdb22fb)


![{displaystyle c[k(s)]=(1-s)y=f[k(s)]-(n g delta )k(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41f9d9e05af64ee209ebc6102b140314de44f9c8)

















