Задача об оптимальном распределении инвестиций
Требуется вложить имеющиеся T единиц средств в 
предприятий, прибыль 
от которых в зависимости от количества вложенных средств 
определяется таблицей, так, чтобы суммарная прибыль со всех предприятий была максимальной.
Здесь — прибыль j-го предприятия при вложении в него 
средств.
Математическая модель задачи будет следующей.
Определить вектор, 
, где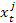 
( 
– количество 
средств вложенных в j-е предприятие, удовлетворяющий условиям
,
и обеспечивающий максимум целевой функции
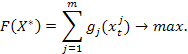
Этап условной оптимизации. Процесс оптимизации разобьем на m шагов и на k-м шаге будем оптимизировать инвестирование в k-е и с k 1 по m-е. При этом последовательно рассматриваются все варианты, когда на инвестирование предприятий с k-го по m-е выделяется сумма 
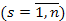, из которых 
достается k-у предприятию, а сумма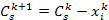 
остается на инвестирование в предприятия с k 1 по m-е. Переменная и будет являться переменной состояния системы на k-м шаге, и может принимать 
возможных значений. Переменной управления на k-м шаге будет величина 
средств, вкладываемых в k-е предприятие. В качестве функций Беллмана 
на k-м шаге в этой задаче можно выбрать максимальную прибыль, которую можно получить от предприятий с k-го по n-е при условии, что на их инвестирование выделяется средств, 
выделяется k-у предприятию. Таким образом, формула для вычисления функций Беллмана на k-м шаге может быть представлена как
На последнем шаге 
, найти функции Беллмана не составляет труда, так как в случае рассматриваются варианты инвестирования 
, и формула имеет вид:
Последовательно проводя вычисления, на шаге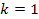 
, мы получим значения функций Беллмана при инвестировании средств в первое и все остальные 
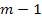предприятия. Так как по условию необходимо инвестировать весь объем средств, то на этом шаге рассматривается только функция Беллмана 
Значение этой функции и будет максимальной прибылью, которую можно получить при инвестировании Т средств в m предприятий.
Этап безусловной оптимизации.На этом этапе в соответствии с алгоритмом обратной прогонки находятся оптимальные управления обеспечивающие максимум функции Беллмана. Так если установлено что на k-м шаге при состоянии системы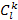 
оптимальное управление есть вложение 
средств в k-е предприятие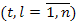 
, то состояние системы на (k 1)-м шаге будет равно 
. Начиная с первого шага, когда 
, можно последовательно восстановить все оптимальные управления .
Модели сетевого планирования и управления
Области применения сетевого планирования и управления
Решение хозяйственных задач связанно с осуществлением ряда работ (действий, мероприятий, операций), одни из которых можно выполнить одновременно, параллельно, а другие – только в определенной последовательности. Например, чтобы начать производство нового изделия, необходимо, прежде всего, разработать его конструкцию, технологию производства, а затем осуществлять четыре вида параллельных работ:
1) проектировать, заказывать, получать и монтировать необходимое оборудование;
2) планировать размещение оборудования, рассчитывать требуемые площади и строить помещения;
3) заключать договора с другими предприятиями о поставках необходимых материалов, сырья и комплектующих деталей;
4) набирать и готовить кадры будущих работников.
В современных условиях необходимо разработать и использовать сравнительно простые и эффективные методы руководства комплексными разработками, вооружить руководителя совершенным инструментом, позволяющим в любых, даже самых сложных ситуациях, быстро принимать наиболее правильные решения.
Поиски более эффективных способов планирования сложных процессов привели к созданию принципиально новых методов сетевого планирования и управления (СПУ). Они применимы в тех случаях, когда конечная цель достигается путем выполнения ряда взаимосвязанных и взаимозависимых работ, входящих в единый комплекс той или иной разработки.
Эффект, достигаемый за счет Сетевого Планирования и Управления, обусловлен в первую очередь внесением строгих логических элементов в формирование плана, позволивших привлечь для анализа и синтеза планов современный математический аппарат и средства вычислительной техники.
В силу универсальности Сетевого Планирования и Управления этот аппарат используется для формирования планов строительной индустрии во всех видах строительства, в индивидуальном и мелкосерийном производстве, в научно-исследовательских, опытно-конструкторских и проектных организациях, в производстве кинофильмов и при разработке народнохозяйственных планов, в горнодобывающей промышленности и геологоразведочных работах.
Сетевой моделью (другие названия: сетевой график, сеть) называется экономико-математическая модель, отражающая комплекс работ (операций) и событий, связанных с реализацией некоторого проекта (научно-исследовательского, производственного и др.), в их логической и технологической последовательности и связи. Анализ сетевой модели, представленной в графической или табличной (матричной) форме, позволяет, во-первых, более четко выявить взаимосвязи этапов реализации проекта и, во-вторых, определить наиболее оптимальный порядок выполнения этих этапов в целях, например, сокращения сроков выполнения всего комплекса работ. Таким образом, методы сетевого моделирования относятся к методам принятия оптимальных решений.
Математический аппарат сетевых моделей базируется на теории графов. Графом называется совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами. Если рассматриваемые пары вершин являются упорядоченными, т. е. на каждом ребре задается направление, то граф называется ориентированным; в противном случае – неориентированным. Последовательность неповторяющихся ребер, ведущая от некоторой вершины к другой, образует путь. Граф называется связным, если для любых двух его вершин существует путь, их соединяющий; в противном случае граф называется несвязным. В экономике чаще всего используются два вида графов: дерево и сеть. Дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины; пути от исходной вершины к крайним вершинам называются ветвями. Сеть – это ориентированный конечный связный граф, имеющий начальную вершину (источник) конечную вершину (сток). Таким образом, сетевая модель представляет собой граф вида «сеть».
В экономических исследованиях сетевые модели возникают при моделировании экономических процессов методами сетевого планирования и управления (СПУ).
Объектом управления в системах СПУ являются коллективы исполнителей, располагающих определенными ресурсами и выполняющих определенный комплекс операций, который призван обеспечить достижение намеченной цели, например, разработку нового изделия, строительства объекта и т. п.
Основой СПУ является сетевая модель (СМ), в которой моделируется совокупность взаимосвязанных работ и событий, отображающих процесс достижения определенной цели. Она может быть представлены в виде графика или таблицы.
Сетевой график.
Важнейшей основой метода Сетевого Планирования и Управления является график.
Сетевой график представляет собой графическое изображение последовательности выполнения комплексной разработки, показывающее взаимосвязь и взаимозависимость отдельных этапов, выполнение которых обеспечивает достижение конечной цели разработки.
Достоинство сетевых графиков заключается в их наглядности и сравнительной простоте исполнения. Сетевые графики позволяют:
a) выявить важнейшие работы, от своевременного выполнения которых зависит соблюдение сроков окончания всей разработки;
b) наглядно представить ход разработки в целом, взаимосвязь и взаимозависимость отдельных этапов разработки;
c) определять общую потребность в рабочей силе и материальных ресурсах для выполнения плана;
d) выявить резервы времени и материальные ресурсы с целью наиболее эффективного выполнения плана;
e) совершенствовать методы планирования и устанавливать строгий ритм в работе;
f) использовать вычислительную технику для расчета показателей сетевых графиков.
Приведенный перечень преимуществ применения методов сетевого планирования и управления дает возможность оценить их огромное мобилизирующее значение как эффективного средства улучшения организации труда и управления производством.
Таким образом, методы Сетевого Планирования и Управления, обеспечивая руководителя необходимой информацией о ходе выполнения разработки, дают ему возможность принимать решения, направленные на достижение максимального эффекта при минимальных затратах времени и ресурсов, поэтому применение методов Сетевого Планирования и Управления близко подходит к возможности разработки оптимальных планов.
Рассмотрим теперь основные термины, применяемые при пользовании сетевыми графиками.
Работа характеризует конкретный этап трудового процесса по выполнению определенной операции комплексной разработки, для чего требуется затраты рабочей силы, материальных ресурсов и времени.
Работа –это любые действия, трудовые процессы, сопровождающиеся затратами ресурсов или времени и приводящие к определенным результатам. На сетевых графах или сетевом графике работы обозначаются стрелками. Для указания того, что одна работа не может выполняться раньше другой, вводятфиктивные работы, которые обозначаются пунктирными стрелками. Продолжительность фиктивной работы принимается равной нулю.
Событиеявляется фактом окончания всех предшествующих данному событию работ, либо началом работ, следующих непосредственно за данным событием. Для совершения события не требуется никаких затрат, а само событие не имеет продолжительности. На сетевом графе события обозначаются в виде вершин графа. Ни одна выходящая из данного события работа не может начаться до окончания всех работ, входящих в это событие.
При составлении сетевого графика необходимо обеспечить логическую последовательность наступления событий, которая определяется взаимосвязью и последовательностью выполнения соответствующих работ.
Приведем следующий простейший график:
Из графика следует, что событие 3 не может наступить, пока не совершится событие 2 и т. д. При этом событие 2 называется последующим по отношению к событию 1, так же как событие 4 является последующим по отношению к событию 3. Событие 3 – предшествующее по отношению к событию 4. В указанных определениях имеется в виду, что события следуют одно за другим и между ними нет промежуточных событий. Одно событие может иметь и несколько предшествующих событий.
Сисходного события(которое не имеет предшествующих работ) начинается выполнение проекта. Завершающим событием(которое не имеет последующих работ) заканчивается выполнение проекта.
Операция – это сама работа или действие. Она обозначается: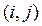 
Это означает, что начальное событие i происходит раньше конечного события j, а длительность операции 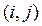, которая обозначается стрелкой, будет равна 
.
Продолжительность выполнения работы измеряется в единицах времени: часах, днях, неделях и т. д.
Любая последовательность работ в сети, в которой конечное событие каждой работы последовательности совпадает с начальным событием следующей за ней работы, называется путем.
Следует различать два вида пути:
1) путем (L) называется непрерывная последовательность выполнения работ от исходного до завершающего события. Продолжительность пути (t) определяется суммой продолжительностей составляющих его работ;
2) критическим путем (Lкр) называется путь от исходного до завершающего события, который имеет максимальную продолжительность (tкр).
Первичный сетевой график составляется на основе исходных (первичных) данных, представленных ответственными исполнителями этапов комплексной работы до его оптимизации.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
Основными временными параметрами сетей являются ранние и поздние сроки наступления (совершения) событий. Зная их, можно вычислить остальные параметры сети – сроки начала и окончания работ и резервы времени событий и работ.
Обозначим – продолжительность работы с начальным событием i и конечным событием j.
Ранний срок
совершения события j определяется величиной наиболее длительного отрезка пути от исходного до рассматриваемого события, причем 
, а 
где N — номер завершающего события. Правило вычисления:
,
где максимум берется по всем событиям i , непосредственно предшествующим событию j (соединены стрелками).
Поздний срок
свершения события i характеризует самый поздний допустимый срок, к которому должно совершится событие, не вызывая при этом срыва срока совершения конечного события. Правило вычисления:
,
где минимум берется по всем событиям j, непосредственно следующим за событием i.
Поздние сроки событий определяются «обратным ходом», начиная с завершающего события, с учетом соотношения 
, т. е. поздний и ранний сроки совершения завершающего события равны между собой.
Резерв
события i показывает, на какой предельно допустимый срок может задержаться свершение события i без нарушения срока наступления завершающего события:
.
События лежащие на критическом пути (критические события) резервов не имеют.
Существуют различные методы расчета параметров сети: табличный и графический.
Рассмотрим графический метод.
При расчетах сетевого графика каждый круг, изображающий событие, делим диаметрами на четыре сектора:
Пример 55. Рассмотрим сеть проекта, представленную следующим графиком.
На графике события представлены кругами, а работы стрелками. Робота может обозначаться как буквой, надписанной на графике рядом с соответствующей работе стрелкой, либо через номера событий из которых начинается и заканчивается работа.
Найти критический путь. Сколько времени потребуется для завершения проекта? Можно ли отложить выполнение роботы D без отсрочки завершения проекта в целом? Насколько недель можно отложить выполнение работы C без отсрочки завершения проекта в целом?
1 этап. При вычислении раннего срока свершения события 
перемещаемся от исходного события 1 завершающему событию 6.
.
В событие 2 входит только одна работа: 
.
Аналогично 
.
В событие 4 входят две работы →
.
.
.
Отсюда следует, что критическое время выполнения проекта = 22.
Внесем соответствующие данные в сетевой график.
2 этап. При вычислении позднего срока tп( i ) свершения события I перемещаемся от завершающего события 6 к исходному событию 1 по сетевому графику против направления стрелок.
.
Далее рассматриваем непосредственно предшествующее событие 5, из которого выходит только одна работа (5 , 6):
.
Из события 4 выходят две работы: (4, 5) и (4, 6). Поэтому определяем поздний срок наступления события tп( 4 ) по каждой из этих работ:
.
.
.
Внесем полученные данные в сетевой график.
3 этап. Вычисляем резерв 
события i , то есть из чисел, полученных на этапе 2, вычитаем числа, полученные на этапе 1.
4 этап. У критических событий резерв времени равен нулю, так как ранние и поздние сроки их свершения совпадают. Критические события 1, 2, 4, 5, 6 и определяют критический путь 1-2-4-5-6, который по определению должен быть самым продолжительным по времени. На сетевом графике мы его покажем двумя чертами.
Теперь можно ответить на вопросы задачи.
Для завершения проекта потребуется 22 недели. Работа D расположена на критическом пути. Поэтому ее нельзя отложить без отсрочки завершения проекта в целом. Работа C не расположена на критическом пути, ее можно задержать на 
(недели).
Сетевое планирование в условиях неопределенности
Продолжительность выполнения работ часто трудно задать точно и потому в практической работе вместо одного числа (детерминированная оценка) задаются две оценки – минимальная и максимальная. Минимальная (оптимистическая) оценка 
характеризует продолжительность выполнения работы при наиболее благоприятных обстоятельствах, а максимальная (пессимистическая) 
— при наиболее неблагоприятных. Продолжительность работы в этом случае рассматривается как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Такие оценки называются вероятностными (случайными), и их ожидаемое значение 
оценивается по формуле (при бета-распределении плотности вероятности):
.
Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии 
:
.
На основе этих оценок можно рассчитать все характеристики СМ, однако они будут иметь иную природу, будут выступать как средние характеристики. При достаточно большом количестве работ модно утверждать (а при малом – лишь предполагать), что общая продолжительность любого, в том числе и критического, пути имеет нормальный закон распределения со средним значением, равным сумме средних значений продолжительности составляющих его работ, и дисперсией, равной суме дисперсий этих же работ.
Кроме обычных характеристик СМ, при вероятностном задании продолжительности работ можно решить две дополнительные задачи:
1) определить вероятность того, что продолжительности критического пути 
не превысит заданного директивного уровня 
;
2) определить максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 
.
Первая задача решается на основе интеграла вероятностей Лапласа 
использованием формулы:
,
где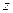 
— нормированное отклонение случайной величины:
;
— среднее квадратичное отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути 
. Дисперсия продолжительности критического пути равна сумме дисперсий работ составляющих критический путь.
Соответствие между 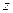и симметричным интегралом вероятностей приведено в таблице. Долее точно соответствие между этими величинами (когда 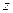вычисляется более чем с одним знаком в дробной части) можно найти в специальной литературе.
Фрагмент таблицы стандартного нормального распределения
|
При достаточно большой полученной величине вероятности (более 0,8) можно с высокой степенью уверенности предполагать своевременное выполнение всего комплекса работ.
Для решения второй задачи используется формула:
.
Кроме описанного выше упрощенного способа расчета сетей с детерминированной структурой и вероятностными оценками продолжительности выполнения работ, используется метод статистических испытаний (метод Монте-Карло). В соответствии с ним на ЭВМ многократно моделируются продолжительности выполнения всех работ и рассчитываются основные характеристики СМ. Большой объем испытаний позволяет более точно выявить закономерности моделируемой сети.
Задача 59.Произвести оптимизацию сетевого графика по ресурсам. Наличный ресурс равен 10.
Найдем критический путь.
Строим график Ганта. В скобках для каждой работы укажем требуемое количество ресурса.
По графику Ганта строим график ресурса. На оси абсцисс мы откладываем время, а на оси ординат – потребности в ресурсах. Считаем, что все работы начинаются в наиболее ранний срок их выполнения. Ресурсы складываются по всем работам, выполняемым одновременно. Также проведем ограничительную линию по ресурсу (в нашем примере это y = 10).
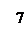
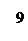
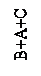
Из графика видно, что на отрезке от 0 до 4, когда одновременно выполняются работы B, A, C, суммарная потребность в ресурсах составляет 3 4 5=12, что превышает ограничение 10. Так как работа C критическая, то необходимо сдвинуть сроки выполнения или A, или B.
Запланируем выполнение работы B с 6-го по 10-й день. На сроках выполнения всего проекта это не скажется и даст возможность остаться в рамках ресурсных ограничений.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
Пусть требуется найти кратчайший маршрут в сети, ведущий от исходного узла к каждому из узлов сети.
Данная задача может быть решена методом присвоения меток. В процессе решения узлам приписываются либо временные, либо постоянные метки. Метка узла называется постоянной – если установлено, что она указывает путь минимальной длины от данного узла до исходного, и временной – если данный факт еще не установлен. Метка, как постоянная, так и временная, имеет два поля значений 
. Число 
метки i-го узла есть расстояние от данного узла до исходного. Число 
есть номер предшествующего узла, через который проходит маршрут длиной . Алгоритм метода присвоения меток состоит из двух этапов.
Первый этап.
1. Исходному узлу, относительно которого определяется кратчайший маршрут, присваивается постоянная метка (0, И). Т. е. значения метки показывают, что данный узел является точкой отсчета маршрута и является исходным узлом сети. Всем узлам, которые непосредственно связаны с исходным узлом (т. е. соединены одним ребром), присваиваются временные метки . Из этих меток постоянной становится та, для которой число минимально. Если меток с минимальным числом несколько, то любую из них можно выбрать в качестве постоянной.
2. Рассматривается очередной узел k, которому присвоена постоянная метка. Всем узлам, которые непосредственно связаны с узлом k и не имеют постоянных меток, присваиваются временные метки, значения которых вычислено от узла k.
3. Из всех временных меток, постоянной становится та, для которой число минимально. Если меток с минимальным числом несколько, то любую из них можно выбрать в качестве постоянной.
4. Алгоритм повторяется, начиная с пункта 2, пока всем узлам не будут присвоены постоянные метки.
Второй этап.
По результатам первого этапа, исходя из значений чисел постоянных меток, восстанавливается маршрут минимальной длины.
Покажем, как исполняется описанный алгоритм, на следующем примере.
Рассмотрим сеть, заданную на рис. 1, с выделенным узлом 1. Цифры на ребрах, связывающих два узла, есть расстояния между этими узлами.
Первый этап.
1-й шаг. Узлу 1 присваиваем постоянную метку (узел с постоянной меткой выделяется, например, более жирной обводкой кружка). Всем узлам, которые соединены с выделенным узлом 1 одним ребром, присваиваем временные метки так, как это показано на рис. 2 – первое число в метке S равно расстоянию от помеченного узла до узла 1, второе число в метке X номер предшествующего узла.
Из полученных временных меток выбираем метку с минимальным первым числом, и делаем ее постоянной, так это показано на рис. 3. Таким образом, по окончании первого шага узлы 1 и 4 имеют постоянные метки, узлы 2 и 3 – временные метки, а узлы 5, 6, 7, 8 и 9 никаких меток не имеют.
2-й шаг. Каждому узлу, который соединен с узлом 4 одним ребром, присваиваем временную метку по следующему правилу:
а) = первое число метки узла 4 длина ребра от узла 4 до соответствующего узла;
б) = 4 указывает на то, что число есть длина пути от исходного узла до рассматриваемого и проходящего через узел 4.
Результат присвоения временных меток представлен на рис. 4. Сравниваем все имеющиеся на данном этапе временные метки. Из них постоянной делаем метку, первое число которой минимально. Это метка узла 3 (16, 1). Делаем ее постоянной (рис. 5).
Замечание: узел 3 имел две временные метки, поэтому вторую метку вычеркиваем или удаляем.
Таким образом, по окончанию второго шага узлы 1, 3 и 4 имеют постоянные метки; узлы 2, 5 и 6 – временные; а узлы 7, 8 и 9 не имеют меток вообще.
3-й шаг. Каждому узлу, не имеющему постоянной метки и непосредственно связанному с узлом 3, присваиваем временную метку по следующему правилу:
а) = первое число метки узла 3 длина ребра от узла 3 до соответствующего узла;
б) = 3 указывает на то, что число есть длина пути от исходного узла до рассматриваемого и проходящего через узел 3.
Результат присвоения временных меток представлен на рис. 6. Сравниваем все имеющиеся на данном этапе временные метки. Из них постоянной делаем метку, первое число которой минимально. Это метка узла 6 (19, 3). Делаем ее постоянной (рис. 7).
По окончанию третьего шага постоянные метки имеют узлы 1, 3, 4 и 6; узлы 2 и 5 – временные; а узлы 7, 8 и 9 не имеют меток.
4-й шаг. Каждому узлу, не имеющему постоянной метки и непосредственно связанному с узлом 6, присваиваем временную метку:
а) = первое число метки узла 6 длина ребра от узла 6 до соответствующего узла;
б) = 6 указывает на то, что число есть длина пути от исходного узла до рассматриваемого и проходящего через узел 6.
Результат присвоения временных меток представлен на рис. 8. Сравниваем все имеющиеся на данном этапе временные метки. Из них постоянной делаем метку, первое число которой минимально. Это метка узла (20, 1). Делаем ее постоянной (рис. 9).
В результате, по окончанию четвертого шага постоянные метки имеют узлы 1, 2, 3, 4 и 6; узлы 5, 7, 8 и 9 – временные.
5-й шаг. Каждому узлу, не имеющему постоянной метки и непосредственно связанному с узлом 2, присваиваем временную метку.
а) = первое число метки узла 2 длина ребра от узла 2 до соответствующего узла;
б) = 2 указывая на то, что число есть длина пути от исходного узла до рассматриваемого и проходящего через узел 2.
Результат присвоения временных меток представлен на рис. 8. Сравниваем все имеющиеся на данном этапе временные метки. Из них постоянной делаем метку, первое число которой минимально. Это метка узла 5 (24, 2). Делаем ее постоянной (рис. 9).
В результате, по окончанию пятого шага постоянные метки имеют узлы 1, 2, 3, 4, 5 и 6; узлы 7, 8 и 9 – временные.
6-й шаг. Каждому узлу, не имеющему постоянной метки и непосредственно связанному с узлом 5, присваиваем временную метку.
Результат присвоения временных меток представлен на рис. 10. Сравниваем все имеющиеся на данном этапе временные метки. Из них постоянной делаем метку, первое число которой минимально. Это метка узла 7 (25, 6). Делаем ее постоянной (рис. 11).
В результате, по окончанию шестого шага постоянные метки имеют узлы 1, 2, 3, 4, 5, 6 и 7; узлы 8 и 9 – временные.
7-й шаг. Каждому узлу, не имеющему постоянной метки и непосредственно связанному с узлом 7, присваиваем временную метку.
Результат присвоения временных меток представлен на рис. 12. Сравниваем все имеющиеся на данном этапе временные метки. Из них постоянной делаем метку, первое число которой минимально. Это метка узла 9 (29, 6). Делаем ее постоянной (рис. 13).
В результате, по окончанию шестого шага постоянные метки имеют узлы 1, 2, 3, 4, 5, 6, 7 и 9; узел 8 – временные.
8-й шаг. Так как узел 9 непосредственно не связан ни с одним узлом, имеющим временные метки, а в сети еще остались узлы, не имеющие постоянных меток, то возвращаемся к рассмотрению узла 7, от которого уже отсчитаны временные метки. Из всех временных меток постоянной делаем ту, первое число которой минимально. Это метка узла 8 (31, 6). Делаем ее постоянной (рис. 14).
В результате, по окончанию восьмого шага все узлы имеют постоянные метки.
Второй этап.
По второму числу метки, от каждого узла находим маршрут до исходного узла, который будет минимальным для данной сети. Покажем это на примере. Рассмотрим узел 8. Второе число в метке, указывает на то, что кратчайший маршрут от узла 1 к узлу 8 лежит через узел 6. Переходим к узлу 6. Второе число метки этого узла показывает, что кратчайший маршрут от узла 1 к узлу 6 лежит через узел 3. Второе число метки узла 3 указывает, что кратчайший путь непосредственно связывает его с узлом 1. Таким образом, кратчайший маршрут от узла 1 к узлу 8 есть: 1-3-6-8.
В результате второго этапа можно сделать вывод, что существуют пять маршрутов соединяющие все узлы сети с узлом 1: а) 1-2-5; б) 1-4; в) 1-3-6-7; г) 1-3-6-8; д)1-3-6-9.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых один и тот же опыт или аналогичные опыты повторяются неоднократно. В результате каждого опыта может появиться или не появиться некоторое событие А, причем нас интересует не результат каждого отдельного опыта, а общее число появлений события А в серии опытов. Например, если производится серия опытов по одной и той же цели, нас, как правило, интересует не результат каждого выстрела, а общее число попаданий. В подобных задачах требуется уметь определять вероятность любого заданного числа появления события в результате серии опытов. Такие задачи решаются весьма просто, если опыты являются независимыми.
Несколько опытов называются независимыми, если вероятность того или иного исхода каждого из опытов не зависят от того, какие исходы имели другие опыты. Например, несколько последовательных бросаний монеты представляют собой независимые опыты. Несколько последовательных выниманий карты из колоды представляют собой независимые опыты при условии, что вынутая карта каждый раз возвращается обратно в колоду и карты перемешиваются; в противном случае – это зависимые опыты. Несколько выстрелов представляют собой независимые опыты только, в случае, если прицеливание производится заново перед каждым выстрелом; в случае, когда прицеливание производится один раз перед всей стрельбой или непрерывно осуществляется в процессе стрельбы выстрелы представляют собой зависимые опыты.
Независимые опыты могут производиться в одинаковых или различных условиях. В первом случаем вероятность события А во всех опытах одна и та же. Во втором случае вероятность события А от опыта к опыту меняется. К первому случаю относится частная теорема, а ко второму – общая теорема о повторении опытов.
Случайные величины и их законы распределения
Ряд распределения
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестное заранее какое именно.
Различают прерывные (дискретные) и непрерывные случайные величины. Возможные значения прерывных величин могут быть заранее перечислены. Возможные значения непрерывных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
Примеры прерывных случайных величин:
1) число появления герба при трех бросаниях монеты (возможные значения 0, 1, 2, 3);
2) частота появления герба в том же опыте (возможные значения 0, 1/3, 2/3, 1);
3) число отказавших элементов в приборе, состоящем из пяти элементов (возможные значения 0, 1, 2, 3, 4, 5);
Примеры непрерывных случайных величин:
1) абсцисса (ордината) точки попадания при выстреле;
2) расстояние от точки попадания до центра мишени;
Условимся в дальнейшем случайные величины обозначать большими буквами, а их возможные значения малыми.
Рассмотрим прерывную случайную величину X с возможными значениями 
, 
, …, 
. Каждое из этих значений возможно, но не достоверно, и величина Х может принять каждое из них с некоторой вероятностью. Обозначим вероятности этих событий буквами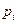 
с соответствующими индексами. Так как события , , …, несовместны и образуют полную группу, то
.
Эта суммарная вероятность каким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана с вероятностной точки зрения, если будет указано какой вероятностью обладает каждое событие , , …, . Этим устанавливается так называемый закон распределения.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Простейшей формой задания закона распределения прерывной случайной величины является таблица в которой перечислен возможные значения случайной величины и соответствующие им вероятности. Такую таблицу называют рядом распределения.
Чтобы придать ряду распределения более наглядный вид, часто прибегают к его графическому изображению: по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат – вероятности этих значений. Для наглядности полученные точки соединяются отрезками прямых. Такая фигура называется многоугольником распределения.
Функция распределения
Ряд распределения, как исчерпывающая характеристика случайной величины
Для количественной характеристики распределения непрерывной случайной величины используется функция распределения которая представляет собой вероятность того что непрерывная случайная величина Х примет значение меньшее х
.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.
Дисперсия и стандартное отклонение
Функция распределения
Для количественной характеристики распределения непрерывной случайной величины используется функция распределения которая представляет собой вероятность того что непрерывная случайная величина Х примет значение меньшее х
.
Теория игр
Пример. Рассмотрим известную всем игру «камень, ножницы, бумага». В эту игру могут играть два человека. Правила игры заключаются в том, что игроки одновременно по команде предъявляют друг другу один из трех имеющихся у каждого игрока предметов: либо камень, либо ножницы, либо бумагу. По правилам игры камень может разбить ножницы, ножницы режут бумагу, бумага накрывает камень. Таким образом, если игрок А предъявляет другому игроку В какой либо из этих предметов, то игрок А может либо выиграть, либо проиграть, либо игра может закончится ничьей в зависимости от того какой из этих трех предметов предъявил в свою очередь игрок В.
В практической деятельности весьма часто приходится рассматривать явления и ситуации, в которых участвуют две или более стороны, имеющие различные интересы и обладающие возможностями применять для достижения своих целей разнообразные действия. Подобные явления и ситуации принято называть конфликтными или просто конфликтами.
Типичный конфликт характеризуется тремя основными составляющими:
1) заинтересованными сторонами,
2) возможными действиями этих сторон,
3) интересами сторон.
Конфликтная ситуация, взятая из реальной жизни, как правило, довольно сложна. К тому же ее изучение затруднено наличием различных обстоятельств, часть из которых не оказывает сколько-нибудь существенного влияния на развития конфликта, ни на его исход. Поэтому для того чтобы анализ конфликтной ситуации оказался возможным, необходимо отвлечение от этих второстепенных факторов, что при удачном стечении обстоятельств позволяет построить упрощенную формализованную модель конфликта, которую и принято называть игрой. От реальной конфликтной ситуации игра отличается еще и тем, что ведется по вполне определенным правилам.
Необходимость изучения и анализа конфликтов, представляемых в виде упрощенных математических моделей (игр), вызвала к жизни специальный математический аппарат – теорию игр.
Опишем некоторые основные понятия, используемые в этой теории.
Заинтересованные стороны называются игроками. Любое возможное для игрока действие (в рамках заданных правил игры) называется его стратегией. В условиях конфликта каждый игрок выбирает свою стратегию, в результате чего складывается набор стратегий, называемый ситуацией. Заинтересованность игроков в ситуации проявляется в том, что каждому игроку в каждой ситуации приписывается число, выражающее степень удовлетворения его интересов в этой ситуации и называемое его выигрышем в ней.
В этих условиях протекание конфликта состоит в выборе каждым игроком своей стратегии и получении им в сложившейся ситуации выигрыша из некоторого источника.
На этом пути создается теория игр с выигрышами.
Однако оценка игроком ситуации путем предположения о своем выигрыше, вообще говоря, не всегда возможна практически и даже не всегда имеет смысл. В подобных случаях иногда удается вместо прямых численных оценок ситуаций указывать на их сравнительную предпочтительность для отдельных игроков.
На этом пути создается теория игр с предпочтениями, включающая в себя и теорию игр с выигрышами.
Тем самым игра – это совокупность правил, описывающих сущность конфликтной ситуации, которые устанавливают:
— выбор образа действия игроков на каждом этапе игры;
— информацию, которой обладает каждый игрок при осуществлении таких выборов;
— плату для каждого игрока после завершения любого этапа игры.
Стратегией игры называется совокупность правил, определяющих поведение игрока от начала игры до ее завершения. Стратегии каждого игрока определяют результаты или платежи в игре. Игра называется с игрой с нулевой суммой, если проигрыш одного игрока равен выигрышу другого, в противном случае она называется игрой с ненулевой суммой.
Игра называется конечной, если у каждого игрока имеется конечное число стратегий.
Если количество игроков равно двум, то игра называется парной, если больше двух, то игра называется множественной. Существуют игры с бесконечным множеством игроков.
Если во множественной игре игроки образуют коалиции, то игра называется коалиционной. Если таких коалиций две, то игра сводится к парной.
Изучение игр можно проводить с различных точек зрения.
Мы будем стремиться
к выработке принципов оптимальности, т. е. того критерия, по которому поведение игроков следует считать оптимальным (разумным, целесообразным);
к выяснению реализуемости этих принципов, т. е. установлению существования оптимальных в выработанном смысле ситуаций, и отысканию этих реализаций.
Одной из плодотворных форм реализации представлений об оптимальности можно считать понятие равновесия, при котором складывается такая (равновесная) ситуация, в нарушении которой не заинтересован ни один из игроков.
Кроме того, ситуации равновесия являются выгодными для каждого игрока: в равновесной ситуации каждый игрок получает наибольший выигрыш (разумеется, в той мере, в какой это от него зависит).
Если в игре ситуации равновесия (в пределах отпущенных возможностей) нет, то, оставаясь в условиях стратегий, имеющихся и игроков, мы сталкиваемся с неразрешимой задачей.
При возникновении подобных случаев естественно ставить вопрос о таком расширении первоначального понятия стратегии, чтобы среди ситуаций, составленных из новых, обобщенных стратегий, заведомо нашлись равновесные.
Если такие обобщенные стратегии существуют, то обычно они представляются некоторыми комбинациями исходных стратегий.
Для того чтобы отличать прежние стратегии от новых, первые называют чистыми, а вторые — смешанными стратегиями.
Весьма плодотворным является представление смешанной стратегии как случайного выбора игроками их чистых стратегий, при котором случайные выборы различных игроков независимы в совокупности, а выигрыш каждого из них определяется как математическое ожидание случайного выигрыша.
Таким образом, преобразованная игра обычно называется смешанным расширением исходной игры.
МАТРИЧНЫЕ ИГРЫ
Рассмотрим игру, в которой участвую два игрока, причем каждый из них имеет конечное число стратегий.
Обозначим для удобства одного из игроков через А, а другого – через В.
Предположим что игрок А имеет m стратегий: 
, 
,…, 
, а игрок B – n стратегий: 
, 
, 
,…, 
.
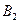Пусть игрок А выбрал стратегию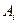 
, а игрок В – стратегию 
.
Будем считать, что выбор игроками стратеги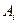й и однозначно определяет исход игры – выигрыш 
игрока А и выигрыш 
игрока В, причем эти выигрыши связаны равенством 
.
Последнее обстоятельство показывает, что в рассматриваемых обстоятельствах выигрыш одного из игроков равен выигрышу другого, взятому с отрицательным знаком, т. е. проигрышу. Поэтому при анализе такой игры можно рассматривать выигрыши только одного из игроков. Пусть это будут, например, выигрыши игрока А.
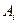Если нам известны значения выигрыша при каждой паре стратегий (в каждой ситуации) и , i = 1, 2, …, m, k = 1, 2, …, n, то их удобно представить записывать
или в виде прямоугольной таблицы, строки которой соответствуют стратегиям игрока А, а столбцы – стратегиям игрока В.
или в виде матрицы
Полученная матрица имеет размер m ´ n и называется матрицей игры или платежной матрицей (отсюда и название игры – матричная).
Рассматриваемую игру часто называют игрой m ´ n или m ´ n-игрой.
Замечание. Матричные игры относятся к разряду так называемых антагонистических игр, т. е. игр, в которых интересы игроков прямо противоположны.
РАВНОВЕСНАЯ СИТУАЦИЯ
Рассмотрим следующий пример.
Два игрока А и В, не глядя друг на друга, кладут на стол по картонному кружку красного (К), зеленного (З) или синего цвета (С), сравнивают цвета кружков и расплачиваются друг с другом так, как показано в матрице игры:
Считая, что эта игра повторяется многократно, попробуем определить оптимальные стратегии каждого из игроков.
Начнем с последовательного анализа стратегии игрока А, не забывая при этом, что его противник, игрок В, может ответить той из своих стратегий, при которой выигрыш игрока А будет минимальным.
Так, на стратегию 
игрока А его противник может ответить стратегией 
(минимальный выигрыш равен – 2, что на самом деле означает проигрыш игрока А, равный 2), на стратегию 
СМЕШАННЫЕ СТРАТЕГИИ
Пример. Швейное предприятие, выпускающее детские платья и костюмы, реализует свою продукцию через фирменный магазин. Сбыт продукции зависит от состояния погоды. По данным прошлых наблюдений предприятие в течение апреля – мая в условиях теплой погоды может реализовать 600 костюмов и 1975 платьев, а при прохладной погоде – 1000 костюмов и 625 платьев. Известно, что затраты на единицу продукции составляют для костюмов 27 ден. ед., для платьев 8 ден. ед., а цена реализации равна соответственно 48 ден. ед. и 16 ден. ед.
Задача заключается в максимизации средней величины прибыли от реализации выпущенной продукции с учетом неопределенности погоды в рассматриваемые месяцы. Таким образом, служба маркетинга предприятия должна в этих условиях определить оптимальную стратегию предприятия, обеспечивающую при любой погоде средний доход. Решим эту задачу методами теории игр, игра в этом случае будет относиться к типу игр с природой.
Предприятие в этих условия располагает двумя чистыми стратегиями: стратегия 
— в расчете на теплую погоду и стратегия 
— в расчете на прохладную погоду. Природу будем рассматривать как второго игрока также с двумя стратегиями: прохладная погода – стратегия 
и теплая погода – стратегия 
. Если предприятие выберет стратегию в расчете на теплую погоду, то в случае прохладной погоды (стратегия природы ) доход составит
руб.,
а в случае теплой погоды (стратегия природы ) доход будет равен
руб.
Если предприятие выберет стратегию в расчете на прохладную погоду, то реализация продукции в условиях прохладной погоды (стратегия природы ) даст доход
руб.,
а в условиях теплой погоды (стратегия природы )
руб.
Следовательно, матрица данной игры (платежная матрица) имеет вид:
.
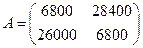Первая и вторая строки этой матрицы стратегиям и предприятия, а первый второй столбцы – стратегиям и природы.
По платежной матрице видно, что первый игрок (предприятие) никогда не получит доход меньшие 6800 руб. Но если погодные условия совпадают с выбранной стратегией, то выигрыш (доход) составит 26000 или 28000 руб. Отсюда можно сделать вывод, что в условиях неопределенности погоды наибольший гарантированный доход предприятие обеспечит, если будет попеременно применять то стратегию , то стратегию . Такая стратегия называется смешанной. Оптимизация смешанной стратегии позволит первому игроку всегда получать среднее значение выигрыша независимо от стратегии второго игрока.
Пусть 
означает частоту применения первым игроком стратегии , тогда частота применения им стратегии равна 
. В случае оптимальной смешанной стратегии первый игрок (предприятие) получит при любой стратегии второго игрока одинаковый средний доход:
.
Отсюда можно найти, что 
; 
.
Следовательно, первый игрок, применяя чистые стратегии и в соотношении 8:9, будет иметь оптимальную смешанную стратегию, обеспечивающую ему в любом случае средний доход в сумме 
руб.; эта величина и будет в данном случае ценой игры.
Легко рассчитать, какое количество костюмов и платьев должно выпускать предприятие при оптимальной смешанной стратегии:
(600 костюмов 1975 платьев) × 8/17 (1000 костюмов 625 платьев) × 9/17 =
= 812 костюмов 1260 платьев.
Следовательно, оптимальная стратегия предприятия заключается в выпуске 812 костюмов и 1260 платьев, что обеспечит ему при любой погоде средний доход в сумме 16965 руб.
В случае когда нижняя цена игры a и верхняя цена игры b не совпадают, 
игрок А может обеспечить себе выигрыш, не меньший a, а игрок В имеет возможность не дать ему больше, чем b.
Возникает вопрос: а как разделить между игроками разность 
?
Предыдущие построения на этот вопрос ответа не дают – тесны рамки возможных действий игроков.
Поэтому довольно ясно, что механизм, обеспечивающий получение каждым из игроков как можно большей доли этой разности, следует искать в определенном расширении стратегических возможностей, имеющихся у игроков изначально.
Оказывается, что компромиссного распределения разности между игроками и уверенного получения каждым игроком своей доли при многократном повторении игры можно достичь путем случайного применения ими своих первоначальных, чистых стратегий.
ИГРА 2´n
Рассмотрим игру с платежной матрицей
Игрок А обладает двумя чистыми стратегиями и , а игрок В – n чистыми стратегиями , , ,…, .
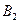Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
Под потоком событий в теории вероятностей понимается последовательность событий, происходящих одно за другим в какие-то моменты времени. Примерами могут служить: поток вызовов на телефонной станции, поток включений приборов в бытовой электросети; поток заказных писем, поступающих в почтовое отделение, поток заявок на обслуживание клиентов, поступающих в склад и т. д. События, образующие поток, в общем виде могут различными, но здесь мы будем рассматривать лишь поток однородных событий, различающихся только моментами появления. Такой поток можно изобразить как последовательность точек 
, 
, …, 
, … на числовой оси, соответствующих моментам появления событий.
Поток событий называется регулярным, если события следуют одно за другим через строго определенные промежутки времени. Такой поток сравнительно редко встречается в реальных системах, но представляет интерес как предельный случай. Типичным для СМО является случайный поток заявок.
Рассмотрим потоки событий, обладающие некоторыми особенно простыми свойствами. Для этого введем ряд определений.
1. Поток событий называется стационарным, если вероятность попадания того или иного числа событий на определенный отрезок времени зависит только от длины этого отрезка и не зависит от того, где именно на числовой оси, характеризующей время, расположен этот участок.
2. Поток событий называется потоком без последствий, если для любых неперекрывающихся отрезков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.
3. Поток событий называется ординарным, если вероятность попадания на элементарный участок 
двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.
Если поток событий обладает всеми тремя свойствами, перечисленными выше, то он называется простейшим (или стационарным пуассоновским) потоком. Название «пуассоновский» связано с тем, что при соблюдении условий 1 – 3 число событий, попадающих на любой фиксированный интервал времени, будет распределено по закону Пуассона.
Рассмотрим подробнее условия 1 – 3, посмотрим, чему они соответствуют для потока заявок и за счет чего они могут нарушаться.
1. Условию стационарности удовлетворяет поток заявок, вероятностные характеристики которого не зависят от времени. В частотности, для стационарного потока характерна постоянная плотность (среднее число заявок в единицу времени). На практике часто встречаются потоки заявок, которые (по крайней мере, на ограниченном отрезке времени) могут рассматриваться как стационарные. Например, поток вызовов на городской телефонной станции на участке времени от 12 до 13 часов может считаться стационарным. Тот же поток в течение целых суток уже не может считаться стационарным (ночью плотность вызовов значительно меньше, чем днем). Заметим, что так обстоит дело и со всеми физическими процессами, которые мы называем «стационарными»: в действительности все они стационарны лишь на ограниченном участке времени, а распространение этого участка до бесконечности – лишь удобный прием, применяемый в целях упрощения анализа. Во многих задачах теории массового обслуживания представляет интерес проанализировать работу системы при постоянных условиях; тогда задача решается для стационарного потока заявок.
2. Условие отсутствия последствия – наиболее существенное для простейшего потока – означает, что заявки поступают в систему независимо друг от друга. Например, поток пассажиров в метро, можно считать потоком без последствий потому, что причины, обусловившие приход отдельного пассажира именно в тот, а не другой момент, как правило, не завязаны с аналогичными причинами для других пассажиров. Однако условие отсутствия последствий может быть легко нарушено за счет появления такой зависимости. Например, поток пассажиров, покидающих станцию метро, уже не может считаться потоком без последствия, так как моменты выхода пассажиров, прибывших одним и тем же поездом, зависимы между собой.
Вообще нужно заметить, что выходной поток (или поток обслуженных заявок), покидающих систему массового обслуживания, обычно имеет последствие, даже если входной поток его не имеет. Последствие, присущее выходному потоку, необходимо учитывать, если этот поток является входным для какой-либо другой системы массового обслуживания (так называемое «многофазовое обслуживание», когда одна и та же заявка последовательно переходит из одной системы в другую).
3. Условие ординарности означает, что заявки приходят по одиночке, а не парами.
Простейший поток играет среди потоков событий вообще особую роль, до некоторой степени аналогичную роли нормального закона среди других законов распределения. Мы знаем, что при суммировании большого числа независимых случайных величин, подчиненных практически любым законом распределения, получается величина, приближенно распределенная по нормальному закону. Аналогично можно доказать, что при суммировании (взаимном наложении) большого числа ординарных, стационарных потоков с практически любым последствием получается поток, сколь угодно близкий к простейшему. Условия, которые должны для этого соблюдаться, аналогичны условиям центральной предельной теоремы, а именно – складываемые потоки должны оказывать на сумму приблизительно равномерно малое влияние.
На практике оказывается обычно достаточно сложить 4 – 5 потоков, чтобы получит поток, с которым можно оперировать как с простейшим.
Простейший поток играет в теории массового обслуживания особую роль. Во-первых, простейшие и близкие к простейшим потоки заявок часто встречаются на практике (причины этого изложены выше). Во-вторых, даже при потоке заявок, отличающемся от простейшего, часто можно получить удовлетворительные по точности результаты, заменив поток любой структуры простейшим с той же плотностью.
Рассмотрим на 
простейший поток событий как неограниченную последовательность случайных точек.
Выделим произвольный участок времени длинной t. Вероятность того, что за время t произойдет ровно m событий, равна
где l — интенсивность потока заявок, т. е. среднее число заявок, приходящихся на единицу времени:
,
где t — среднее значение интервала между двумя соседними заявками.
В частности, вероятность того, что отрезок окажется пустым (не произойдет ни одного события), будет равна
Важной характеристикой потока является закон распределения длины промежутка между соседними событиями. Рассмотрим случайную величину T – промежуток времени между произвольными двумя соседними событиями в простейшем потоке и найдем ее функцию распределения
.
Перейдем к вероятности противоположного события
.
Это есть вероятность того, что на отрезке времени длиной t, начинающемся в момент появления одного из событий потока, не появится ни одного из последующих событий. Так как простейший поток не обладает последствием, то наличие в начале отрезка (в точке ) какого-то события никак не влияет на вероятность появления других событий в дальнейшем. Поэтому вероятность 
можно вычислить по формуле
,
откуда
.
Дифференцируя, найдем плотность распределения
. (*)
Закон распределения с плотностью (*) называется показательным законом, а величина 
— его параметром.
Математическое ожидание, дисперсия и среднеквадратическое отклонение для случайной величины распределенной по показательному закону соответственно равны
, 
, 
.
Показательный закон распределения обладает одним замечательным свойством, а именно: если промежуток времени, распределенный по показательному закону, уже длился некоторое время, то это никак не влияет на закон распределения оставшейся части промежутка.
Время обслуживания.
Кроме характеристик входного потока заявок, режим работы системы зависит еще от характеристик производительности самой системы: числа каналов n и быстродействия каждого канала. Одной из важнейших величин, связанных с системой, является время обслуживания одной заявки 
. Эта величина может быть как неслучайной, так и случайной. Очевидно, более общим является случайное время обслуживания.
Рассмотрим случайную величину и обозначим 
ее функцию распределения:
.
а 
— плотность распределения:
.
Для практики особый интерес представляет случай, когда величина имеет показательный закон распределения
где параметр m — интенсивность потока обслуживания, величина, обратная среднему времени обслуживания одной заявки:
,
где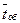 
— среднее время обслуживания.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
Рассмотрим задачу с использованием СМО с отказами.
Пример 1. В ОТК цеха работают три контролера. Если деталь поступает в ОТК, когда все контролеры заняты обслуживанием ранее поступивших деталей, то она проходит отдел непроверенной. Среднее число деталей, поступающих в ОТК в течение часа, равно 24, среднее время, которое затрачивает контролер на обслуживание одной детали, равно 5 мин. Определить вероятность того, что деталь пройдет ОТК необслуженной, насколько загружены контролеры и сколько их необходимо поставить, чтобы 
(* — заданное значение 
).
Решение: По условию задачи 
, 
мин, тогда 
, 
.
1. Вероятность простоя каналов, когда нет заявок:
.
2. Вероятность отказа в обслуживание, когда все каналы заняты:
.
3. Вероятность обслуживания, т. е. вероятность того, что свободен хотя бы один канал:
.
4. Среднее число занятых обслуживанием каналов:
.
5. Абсолютная пропускная способность
При 
.
Произведем аналогичные расчеты при 
:
1. Вероятность простоя каналов, когда нет заявок:
.
2. Вероятность отказа в обслуживание, когда все каналы заняты:
.
3. Вероятность обслуживания, т. е. вероятность того, что свободен хотя бы один канал:
.
При 
.
Произведем аналогичные расчеты при 
:
4. Вероятность простоя каналов, когда нет заявок:
.
5. Вероятность отказа в обслуживание, когда все каналы заняты:
.
6. Вероятность обслуживания, т. е. вероятность того, что свободен хотя бы один канал:
.
При 
.
Ответ. Вероятность того, что при деталь пройдет ОТК необслуженной, составляет 21%, и контролеры будут загружены обслуживанием на 53%.
Чтобы обеспечить вероятность обслуживания более 95%, необходимо не менее пяти контролеров.
Рассмотрим задачу с использованием СМО с неограниченным ожиданием.
Пример 2. Сберкасса имеет трех контролеров-кассиров для обслуживания вкладчиков. Каждый день в сберкассу обращается за обслуживанием в среднем около 240 человек. Рабочий день длится 8 часов. Средняя продолжительность обслуживания контролером-кассиром одного вкладчика 3 мин.
Определить характеристики сберкассы как объекта СМО.
Решение. По условию задачи , 
, 
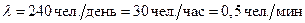, тогда 
, 
. Так как 
, следовательно, в СМО существует установившийся режим работы.
1. Вероятность простоя каналов, когда нет заявок:
.
2. Вероятность того, что все каналы заняты обслуживанием:
.
3. Среднее число занятых каналов:
.
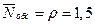4. Среднее число свободных каналов:
.
5. Среднее число заявок находящихся в очереди:
.
6. Среднее число заявок находящихся в системе:
7. Среднее время ожидания заявки в очереди на обслуживание:
мин.
8. Среднее время пребывания заявки в СМО:
мин.
Ответ. Вероятность простоя контролеров-кассиров равна 21% рабочего времени, вероятность посетителю оказаться в очереди составляет 11,8%, среднее число посетителей в очереди 0,236 чел., среднее время ожидания посетителями обслуживания 0,472 мин.
Рассмотрим задачу с применением СМО с ожиданием и с ограничением на длину очереди.
Пример 3. На автозаправочной станции установлены 3 бензоколонки. Около станции находится площадка на 3 автомобиля для ожидания заправки, в случае если бензоколонки заняты. В течение часа на автозаправочную станцию пребывает в среднем 75 автомобилей. Среднее время обслуживания одного автомобиля 2 мин.
Определить все характеристики автозаправочной станции как объекта СМО. Какова должна быть вместимость площадки для ожидания обслуживания, чтобы заданная вероятность обслуживания 
.
Решение. По условию задачи , 
, 
, 
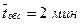, тогда 
, 
.
1. Вероятность простоя каналов, когда нет заявок:
2. Вероятность отказа в обслуживании:
3. Вероятность обслуживания:
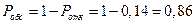
4. Абсолютная пропускная способность:
5. Среднее число занятых каналов:
6. Среднее число свободных каналов:
7. Среднее число заявок находящихся в очереди:
8. Среднее число заявок находящихся в системе:
9. Среднее время ожидания обслуживания:
10. Среднее время ожидания заявки в очереди на обслуживание:
11. Среднее время пребывания заявки в СМО:
При 
.
Произведем аналогичные расчеты при 
:
1. Вероятность простоя каналов, когда нет заявок:
2. Вероятность отказа в обслуживании:
3. Вероятность обслуживания:
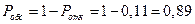
При 
.
Произведем аналогичные расчеты при 
:
1. Вероятность простоя каналов, когда нет заявок:
2. Вероятность отказа в обслуживании:
3. Вероятность обслуживания:
При 
.
Ответ. Вероятность того, что при автомобиль будет обслужен автозаправочной станцией составляет 86%. Чтобы обеспечить вероятность обслуживания более 90%, необходимо не менее пяти мест ожидания заправки.
МЕТОДЫ ПРОГНОЗИРОВАНИЯ
Временные ряды
Данные за прошлые периоды можно использовать для прогнозирования.
Множество данных, где время является независимой переменной, называется временным рядом.
Общее изменение со временем результативного признака называется трендом. Мы рассмотрим модели линейного тренда, то есть параметры тренда модно рассчитать с помощью модели линейной регрессии.
Сезонная вариация – это повторение данных через небольшой промежуток времени. Под «сезоном» можно понимать день, и неделю, и месяц, и квартал. Если же промежуток времени будет длительным, то это – циклическая вариация. Мы остановимся на изучении данных для небольших интервалов времени, поэтому циклическую вариацию исключим из рассмотрения.
Сначала на основании прошлых данных определяется сезонная вариация. Исключив сезонную вариацию (проведя так называемую десезонализацию данных), с помощью модели линейной регрессии находим уравнение тренда. По уравнению тренда и прошлым данным вычисляем величины ошибок. Это среднее абсолютное отклонение 
и среднеквадратическая ошибка 
, где 
— это разность фактического и прогнозного значений в момент времени t , n – число наблюдений.
Анализ аддитивной модели.
Для аддитивной модели фактическое значение фактическое значение A = трендовое значение T сезонная вариация S ошибка E.
Пример 50. Предположим, что нам известен объем прожаж (тыс. руб.) за последние 11 кварталов. Дадим на основании этих данных прогноз объема продаж на следующие два квартала.
На первом шаге нужно исключить влияние сезонной вариации. Воспользуемся методом скользящей средней. Заполним таблицу.
| Номер квартала | Объем продаж | Скользящая средняя за 4 квартала | Центрированная скользящая средняя | Оценка сезонной вариации |
| 4,75 | 5,5 | — 1,5 | ||
| 6,25 | 6,5 | — 1,5 | ||
| 6,75 | 7,125 | 2,875 | ||
| 7,5 | ||||
| 8,5 | 8,75 | — 1,75 | ||
| 9,75 | — 0,75 | |||
| 10,5 | 11,5 | 0,5 | ||
| 12,5 | ||||
1 год = 4 квартала. Поэтому найдем среднее значение объема продаж за 4 последовательных квартала. Для этого нужно сложить 4 последовательных числа из 2-го столбца (объем продаж), эту сумму умножить на 4 (количество слагаемых) и результат записать в 3-й столбец напротив 3-го слагаемого.
Если при заполнении 3-го скользящая средняя вычислялась для четного числа сезонов, то вычисляется центрированная скользящая средняя по следующему правилу: полусумму двух соседних чисел из 3-го столбца запишем в четвертый столбец напротив верхнего из них. В противном случае (если скользящая средняя вычислялась для нечетного числа сезонов) центрированную скользящую среднюю вычислять не надо.
5-й столбец (оценка сезонной вариации) – это разность объема продаж и скользящей средней, в случае если последняя вычислялась для нечетно числа сезонов или разность объема продаж и центрированной скользящей средней в противном случае.
Заполним следующую таблицу. Оценки сезонной вариации запишем под соответствующим номером квартала году. В каждом столбце вычисляем среднее значение оценок сезонной вариации = (сумма чисел в столбце)/ (количество чисел в столбце). Результат запишем в строке «Среднее» (округления взяты до одной цифры после запятой). Сумма чисел в строке «Среднее» = -1.
Скорректируем значения в строке «Среднее», чтобы общая сумма была равна 0. Это необходимо, чтобы усреднить значения сезонной вариации в целом за год. Корректирующий фактор вычисляется следующим образом: сумма оценок сезонных вариаций (-1) делится на число кварталов в году (4). Поэтому из каждого числа этой строки нужно вычесть -1/4= -0,25. Так как у нас округления до одной цифры после запятой, то из нечетных столбцов вычтем -0,3, а из четных столбцов вычтем -0,2. В последней строке получены значения сезонной вариации для соответствующего квартала года.
| Номер квартала в году | |||||
| -1,5 | -1,5 | ||||
| 2,875 | -1,75 | -0,75 | |||
| 0,5 | среднее | ||||
| Среднее | 1,7 | 0,0 | -1,6 | -1,1 | -1 |
| Скорректированная сезонная вариация | 2,0 | 0,2 | -1,3 | -0,9 | 0,0 |
Исключим сезонную вариацию из фактических данных. Проведем десезонализацию данных.
| Номер квартала | Объем продаж A | Сезонная вариация S | Десезонализированный объем продаж A-S=T E |
| 0.2 | 5.8 | ||
| -1,3 | 5,3 | ||
| -0,9 | 5,9 | ||
| 0,2 | 7,8 | ||
| -1,3 | 8,3 | ||
| -0,9 | 9,9 | ||
| 0,2 | 13,8 | ||
| -1,3 | 16,3 |
Из чисел 2-го столбца вычитаем числа 3-го столбца и результат пишем в 4-м столбце.
Уравнение линии тренда T=a b*x, где 
— номер i— го квартала.
Найдем коэффициенты a и b по данным следующим формулам:
где — номер i— го квартала, а 
— значение сезонной вариации i— го квартала.
Для упрощения расчетов по указанным формулам заполним таблицу
| Номер квартала | x | y | x2 | xy |
| 5,8 | 11,6 | |||
| 5,3 | 15,9 | |||
| 5,9 | 23,6 | |||
| 7,8 | 46,8 | |||
| 8,3 | 58,1 | |||
| 9,9 | 79,2 | |||
| 13,8 | ||||
| 16,3 | 179,3 | |||
| Сумма | 93,1 | 684,5 |
Подставляя соответствующие данные из таблицы в приведенные выше формулы получим: a=1,9и b=1,1.
Итак, уравнение тренда запишется так T=1,9 1,1 x.
Теперь займемся расчетом ошибок.
Для этого необходимо найти величины 
— разность фактического и прогнозного значения в i-ом квартале по следующей формуле:
, где 
— объем продаж, 
— сезонная вариация, 
— трендовое значение в i-ом квартале.
Чтобы вычислить трендовое значение в i-ом квартале воспользуемся соответствующей формулой приведенной выше подставляя в нее вместо x номер соответствующего квартала.
Составим таблицу
| № квар. | Объем продаж A | Десезонализированный объем продаж A-S=T E | Трендовое значение | Ошибка |  |  |
| -1 | ||||||
| 5,8 | 4,1 | 1,7 | 1,7 | 2,89 | ||
| 5,3 | 5,2 | 0,1 | 0,1 | 0,01 | ||
| 5,9 | 6,3 | -0,4 | 0,4 | 0,16 | ||
| 7,4 | 0,6 | 0,6 | 0,36 | |||
| 7,8 | 8,5 | -0,7 | 0,7 | 0,49 | ||
| 8,3 | 9,6 | -1,3 | 1,3 | 1,69 | ||
| 9,9 | 10,7 | -0,8 | 0,8 | 0,64 | ||
| 11,8 | -1,8 | 1,8 | 3,24 | |||
| 13,8 | 12,9 | 0,9 | 0,9 | 0,81 | ||
| 16,3 | 2,3 | 2,3 | 5,29 | |||
| Сумма | 11,6 | 16,58 |
Среднее абсолютное отклонение 
и среднеквадратическая ошибка 
. Мы видим, что ошибки достаточно велики. Это скажется на качестве прогноза.
Дадим прогноз объема продаж на следующие два квартала.
прогноз = трендовое значение скорректированная сезонная вариация.
Мы считаем, что тенденция, выявленная по прошлым данным, сохранится и в ближайшем будущем. Подставляем номера кварталов в формулу и учитываем скорректированную сезонную вариацию.
Прогноз объема продаж в 12-м квартале: (1,9 1,1*12) (-0,9)=14,2 тыс.руб.
Прогноз объема продаж в 13-м квартале: (1,9 1,1*13) 2=18,2 тыс.руб.
Задача 50. В таблице указан объем продаж (тыс. руб.) за последние 11 кварталов. Дать на основании этих данных прогноз объема продаж на следующие два квартала.
На первом шаге нужно исключить влияние сезонной вариации. Воспользуемся методом скользящей средней. Заполним таблицу.
| Номер квартала | Объем продаж | Скользящая средняя за 4 квартала | Центрированная скользящая средняя | Оценка сезонной вариации |
| 5,625 | -0,625 | |||
| 6,25 | 6,75 | -0,75 | ||
| 7,25 | 7,625 | 1,375 | ||
| 8,5 | 0,5 | |||
| 9,25 | -1,25 | |||
| 9,5 | ||||
| 10,5 | 11,5 | -0,5 | ||
| 12,5 | ||||
1 год = 4 квартала. Поэтому найдем среднее значение объема продаж за 4 последовательных квартала. Для этого нужно сложить 4 последовательных числа из 2-го столбца (объем продаж), эту сумму умножить на 4 (количество слагаемых) и результат записать в 3-й столбец напротив 3-го слагаемого.
Если при заполнении 3-го скользящая средняя вычислялась для четного числа сезонов, то вычисляется центрированная скользящая средняя по следующему правилу: полусумму двух соседних чисел из 3-го столбца запишем в четвертый столбец напротив верхнего из них. В противном случае (если скользящая средняя вычислялась для нечетного числа сезонов) центрированную скользящую среднюю вычислять не надо.
5-й столбец (оценка сезонной вариации) – это разность объема продаж и скользящей средней, в случае если последняя вычислялась для нечетно числа сезонов или разность объема продаж и центрированной скользящей средней в противном случае.
Заполним следующую таблицу. Оценки сезонной вариации запишем под соответствующим номером квартала году. В каждом столбце вычисляем среднее значение оценок сезонной вариации = (сумма чисел в столбце)/ (количество чисел в столбце). Результат запишем в строке «Среднее» (округления взяты до одной цифры после запятой). Сумма чисел в строке «Среднее» .
Скорректируем значения в строке «Среднее», чтобы общая сумма была равна 0. Это необходимо, чтобы усреднить значения сезонной вариации в целом за год. Корректирующий фактор вычисляется следующим образом: сумма оценок сезонных вариаций. Поэтому из каждого числа этой строки нужно вычесть = 0,593. В последней строке получены значения сезонной вариации для соответствующего квартала года.
| Номер квартала в году | |||||
| -0,625 | -0,75 | ||||
| 1,375 | 0,5 | -1,25 | |||
| -0,5 | среднее | ||||
| Среднее | 1,125 | 0,5 | -0,938 | -0,375 | 0,078 |
| Скорректированная сезонная вариация | 1,047 | 0,422 | -1,016 | -0,453 | 0,0 |
Исключим сезонную вариацию из фактических данных. Проведем десезонализацию данных.
| Номер квартала | Объем продаж A | Сезонная вариация S | Десезонализированный объем продаж A-S=T E |
| 1,047 | 2,953 | ||
| 0,422 | 4,578 | ||
| -1,016 | 6,016 | ||
| -0,453 | 6,453 | ||
| 1,047 | 7,953 | ||
| 0,422 | 8,578 | ||
| -1,016 | 9,016 | ||
| -0,453 | 10,453 | ||
| 1,047 | 9,953 | ||
| 0,422 | 12,578 | ||
| -1,016 | 17,016 |
Из чисел 2-го столбца вычитаем числа 3-го столбца и результат пишем в 4-м столбце.
Уравнение линии тренда T=a b*x, где — номер i— го квартала.
Найдем коэффициенты a и b по данным следующим формулам:
где — номер i— го квартала, а — значение сезонной вариации i— го квартала.
Для упрощения расчетов по указанным формулам заполним таблицу
| Номер квартала | x | y | x2 | xy |
| 2,953 | 2,953 | |||
| 4,578 | 9,156 | |||
| 6,016 | 18,048 | |||
| 6,453 | 25,812 | |||
| 7,953 | 39,765 | |||
| 8,578 | 51,468 | |||
| 9,016 | 63,112 | |||
| 10,453 | 83,624 | |||
| 9,953 | 89,577 | |||
| 12,578 | 125,78 | |||
| 17,016 | 187,176 | |||
| Сумма | 95,547 | 696,471 |
Подставляя соответствующие данные из таблицы в приведенные выше формулы получим: a=1,97и b=1,12.
Итак, уравнение тренда запишется так T=1,97 1,12 x.
Теперь займемся расчетом ошибок.
Для этого необходимо найти величины — разность фактического и прогнозного значения в i-ом квартале по следующей формуле:
, где — объем продаж, — сезонная вариация, — трендовое значение в i-ом квартале.
Чтобы вычислить трендовое значение в i-ом квартале воспользуемся соответствующей формулой приведенной выше подставляя в нее вместо x номер соответствующего квартала.
Составим таблицу
| № квар. | Объем продаж A | Десезонализированный объем продаж A-S=T E | Трендовое значение | Ошибка | | |
| 2,953 | 2,240 | 0,713 | 0,713 | 0,507 | ||
| 4,578 | 4,206 | 0,372 | 0,372 | 0,138 | ||
| 6,016 | 5,326 | 0,690 | 0,690 | 0,476 | ||
| 6,453 | 6,446 | 0,007 | 0,007 | 4,5E-05 | ||
| 7,953 | 7,566 | 0,387 | 0,387 | 0,150 | ||
| 8,578 | 8,686 | -0,108 | 0,108 | 0,012 | ||
| 9,016 | 9,806 | -0,790 | 0,790 | 0,624 | ||
| 10,453 | 10,926 | -0,473 | 0,473 | 0,224 | ||
| 9,953 | 12,046 | -2,093 | 2,093 | 4,380 | ||
| 12,578 | 13,166 | -0,588 | 0,588 | 0,345 | ||
| 17,016 | 14,286 | 2,730 | 2,730 | 7,455 | ||
| Сумма | 8,950 | 14,312 |
Среднее абсолютное отклонение 
и среднеквадратическая ошибка 
. Мы видим, что ошибки достаточно велики. Это скажется на качестве прогноза.
Дадим прогноз объема продаж на следующие два квартала.
прогноз = трендовое значение скорректированная сезонная вариация.
Мы считаем, что тенденция, выявленная по прошлым данным, сохранится и в ближайшем будущем. Подставляем номера кварталов в формулу и учитываем скорректированную сезонную вариацию. T=1,97 1,12 x.
Прогноз объема продаж в 12-м квартале: (1,97 1,12*12) ( -0,453)=14,957 тыс.руб.
Прогноз объема продаж в 13-м квартале: (1,97 1,12*13) 1,047=17,577 тыс.руб.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Экономико-математическая модель оптимального распределения инвестиций при модернизации наукоёмких предприятий
Чурсин А. А., Шмаков Е. В.
ЭКОНОМИКО-МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ИНВЕСТИЦИЙ
18. МАТЕМАТИЧЕСКИЕ МЕТОДЫ И ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
18.1. ЭКОНОМИКОМАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ИНВЕСТИЦИЙ ПРИ МОДЕРНИЗАЦИИ НАУКОЁМКИХ ПРЕДПРИЯТИЙ1
Чурсин Александр Александрович, директор Института прикладных технико-экономических исследований и экспертиз, заведующий кафедрой «Прикладная экономика» Российского университета дружбы народов,
д.э.н., профессор
Место работы: Институт прикладных техникоэкономических исследований и экспертиз; РУДН
achursin2008@yandex.ru
Шмаков Евгений Вячеславович, начальник центра технической информации и анализа применения электронной компонентной базы ОАО «Российские космические системы», PMP
Место работы: ОАО «Российские космические системы», PMP
evgeny@shmakov.pro
Аннотация: Цель написания настоящей статьи заключается в попытке более объективно взглянуть на проблему имитационного моделирования результатов инвестиционных вложений в модернизацию предприятий, работающих в инновационных отраслях экономики. Важность внедрения инноваций для получения высокого экономического эффекта подчёркивается многими и в том числе на уровне правительства. В качестве примера можно привести американскую политику для предприятий в области совместных исследований [4].
При построении экономико-математической модели были использованы метод декомпозиции для идентификации основных компонентов модели и метод математического программирования для установления зависимости между компонентами модели, т.е. для её решения.
Предложенная экономико-математическая модель распределения инвестиций при модернизации наукоёмких предприятий позволяет оптимальным образом распределять инвестиции между тремя основными затратными статьями: трудовыми ресурсами, используемыми при производстве материалами и оборудованием. Оптимальное распределение инвестиций, позволит сэкономить финансовые ресурсы предприятия, поднять квалификацию тех работников, которые действительно нуждаются в повышении квалификации с точки зрения производства продукции, а так же модернизировать те производственные мощности, которые дадут наибольший вклад в повышение конкурентоспособности и финансовой устойчивости предприятия.
Предложенная модель может быть детализирована и масштабируема в зависимости от цели модернизации и масштаба предприятия.
Практическая ценность от внедрения данной модели при распределении инвестиций заключается в фокусировании
1 Исследование подготовлено при финансовой поддержке Российского гуманитарного научного фонда, грант №14-02-00443 «Разработка теоретических подходов к выбору наиболее эффективных путей реструктуризации ракетно-космической промышленности России в современных условиях».
внимания инвесторов (как внешних, так и внутренних) на главный продукт предприятия и модернизацию того, что вносит наибольший вклад в увеличение ценности главного продукта.
Предложенная экономико-математическая модель оптимального распределения инвестиций при модернизации наукоёмких предприятий может быть полезна в первую очередь директорам и менеджерам высшего звена предприятий, принимающим решение о необходимости модернизации предприятия и выделении для этого соответствующих ресурсов
Ключевые слова: модель, инвестиции, наукоемкие отрасли, модернизация, трудовые ресурсы
ECONOMIC-MATHEMATICAL MODEL OF OPTIMUM DISTRIBUTION OF INVESTMENTS AT MODERNIZATION OF THE KNOWLEDGE-INTENSIVE ENTERPRISES
Chursin Alexander, PhD in Economics, Professor, Director of the Institute of Applied Technical and Economic Research and Expert. Assessment of Peoples’ Friendship University of Russia
Work place: the Institute of Applied Technical and Economic Research and Expert; Peoples’ Friendship University of Russia
achursin2008@yandex.ru
Shmakov Evgeny, Head of Department of Technical Information and Analysis of Application of Electronic Components of Russian Space Systems
Work place: Electronic Components of Russian Space Systems
evgeny@shmakov.pro
Annotation: The purpose of this article writing is an attempt to look more objectively at the problem of imitation modeling of the results of investments in enterprise modernization which function in innovative branches of economy. Importance of innovation introduction for receiving high economic effect is widely acknowledged and on the level of the government as well. American policy for enterprises in the sphere of joint research can be given as an example [4].
The method of decomposition for identification of main model components and the method of mathematical programming for establishment of dependence between model components, i.e. for its solution were used for building of an economic and mathematical model.
The suggested economic and mathematical model of investment distribution during modernization of knowledge-intensive enterprises allows optimal distribution of investments among three main expensive items: labour force, materials and equipment used in production. Optimal distribution of investments will allow saving financial resources of an enterprise, advancing qualification of those employees who really need further training from the point of view of production manufacturing as well as modernizing those production facilities which will make the largest contribution into competitive recovery and financial stability of an enterprise. The suggested model can be detailed and scaled depending on modernization purpose and scale of an enterprise.
239
Бизнес в законе
3’2021
Practical value of this model introduction during investment distribution is drawing investors’ (external as well as domestic ones) attention on the main product of an enterprise and modernization of items that have contributed to the utmost in raising of main product value.
The suggested economic and mathematical model of optimal investment distribution during modernization of science-driven enterprises can be useful first of all to directors and top managers of enterprises that have made a decision of the necessity in enterprise modernization and allocation of the corresponding funds on it
Keywords: model, investments, knowledge-intensive
branches, modernization, labour force
В сегодняшних непростых условиях наблюдающегося спада мировой и отечественной экономики, проходящего секвестра государственных программ и, соответственно, стремительно сокращающегося бюджета многих предприятий, актуальной вновь становится проблема финансовой устойчивости и модернизации предприятий.
Проблемам финансовой устойчивости в большей степени подвержены предприятия и организации, выпускающие неконкурентную продукцию и/или имеющие не диверсифицированное производство. Такими предприятиями и организациями, как правило, выступают предприятия государственного сектора экономики. Примером могут служить предприятия оборонной и ракетно-космической промышленности, которые по сравнению со своими западными конкурентами имеют крайне слабую диверсификацию производства.
Одним из эффективных способов приобретения финансовой устойчивости является модернизация предприятия и переход на выпуск конкурентно способной продукции. Это отмечается всеми авторами, в том числе зарубежными [4].
На этом этапе возникает множество проблем, для решения которых мы предлагаем использовать экономико-математическую модель распределения инвестиций при модернизации наукоёмких предприятий.
Вопросы построения и анализа экономико-
математических моделей исследуются в ряде научных публикаций. В основном, описываемые в литературе, экономико-математические модели применяются для оценки инновационного потенциала предприятия, поэтому при описании нашей математической модели будем опираться именно на них.
В работе [2] рассматривается экономико-
математическая модель инновационной привлекательности продукции предприятия, как функция её потребительских свойств. При этом отмечается, что большинство инноваций связано не с разработкой принципиально новых технико-технологических решений, а с усовершенствованием уже существующих. В данной работе предлагается взглянуть на продукцию, как на набор определённых потребительских свойств, ценность которых известна покупателю. Соответственно инновационную деятельность предприятия автор рассматривает, как улучшение тех или иных потребительских свойств выпускаемой продукции. В данной работе разработана формула комплексной количественной оценки потребительских свойств продукции предприятия, которая имеет вид:
tt, > 0 , ^ а, = 1,
Г = 1
где Ри р° — значения параметра потребительского свойства / анализируемой продукции и её наилучшего аналога (базового образца) соответственно, Щ — коэффициент значимости данного потребительского свойства, n — число рассматриваемых параметров (потребительских свойств) продукции.
В работе [1] приведена, разработанная на основе (1), экономико-математическая модель задачи оптимизации инновационной деятельности (точнее, некоторых её аспектов) промышленного предприятия. Авторы утверждают, что инновационная деятельность предприятия по улучшению потребительских свойств продукта приводит к изменению значений их параметров на некоторую величину й о i что находит отражение в увеличении показателя его инновационного уровня:
Vi т
vl
(2)
Равенство *Рг = » означает, что данные потребительские свойства i по тем или иным причинам не было улучшено в результате соответствующих инновационных процессов. При этом авторы делают следующее допущение: инновационная деятельность по улучшению одних потребительских свойств не приводит к ухудшению других, и значит все &Pi ^ °.
Далее авторы вводят понятие затраты (в денежном эквиваленте) Ч на усовершенствование /-го потребительского свойства, как функцию от изменения параметра приращения потребительского свойства: zi = ziCAPt). Тогда общие затраты Z на совершенствование определённого вида продукции (соответствующих его потребительских свойств) будут определяться соотношением:
С учётом вышеизложенного В.А. Диленко и С.А. Шпак конкретизируют задачу оптимизации инновационной деятельности промышленного предприятия и сводят её к определению (в рамках имеющих финансовых возможностей) комплекса инновационных мероприятий по совершенствованию потребительских свойств выпускаемой продукции с целью максимизации возможного дохода от её реализации:
где функция ckt_uk) определяет цену продукции вида к с инновационным уровнем ик {k=i,….m)i а — ожидаемый объём её реализации (в натуральных единицах);
p«l- Рл — значения параметра потребительского свойства i продукции вида k данного предприятия и её базового образца соответственно;
— величина изменения (улучшения) параметра потребительского свойства i продукции k в результате реализации соответствующего инновационного мероприятия;
ат — весовой коэффициент значимости параметра / (соответствующего потребительского свойства) в об-
240
Чурсин А. А., Шмаков Е. В.
ЭКОНОМИКО-МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ИНВЕСТИЦИЙ
щей количественной оценке инновационного уровня продукции вида к
пк — число анализируемых потребительских свойств (параметров) продукции вида к при количественной оценке её инновационного уровня;
zife(*Pik) — функция величины затрат, возникающих в связи с изменением значения параметра / продукции вида к на величину лРт;
h — перечень потребительских свойств продукции вида к, которые могут быть усовершенствованы;
/ — множество видов продукции предприятия, из которых хотя бы одно потребительское свойство можно улучшить;
— объём финансовых средств, выделенных на совершенствование продукции вида к
&Pik — величина максимально возможного изменения значения параметра i продукции вида к в результате осуществления соответствующего инновационного мероприятия.
В приведённой выше модели функция (4) предполагает максимизацию суммарного дохода предприятия от продажи выпускаемой продукции за счёт реализации инновационных мероприятий по совершенствованию её потребительских свойств.
Основной недостаток всех описанных выше моделей заключается в том, что они рассматривают конкурентоспособность в статическом виде без учёта временного фактора.
Данная проблема решена в работе [3], где вопросы конкурентоспособности рассматриваются в динамике:
Т-п=1 Отп$УЧпЮ _
(ГГ,(1,1) (t) > о,
1,1= ;
4._,N|2:
(8)
(9)
(10)
*ТСО =
K£i,2rm>».
Sj,(n
где » X.® — коэффициент конкурентоспособности продукции по ч-му частному показателю;
su и — ъ-й показатель потребности покупателей (параметр рассматриваемого товара) и его базовый аналог соответственно;
Wi — количество частных показателей конкурентоспособности продукции;
к, (£}= ДЦВ.
’ — коэффициент конкурентоспособности
продукции по ii-му частному научно-техническому показателю;
si,H siI» — ъ-й частный показатель потребности покупателей (частный параметр рассматриваемого товара) и его базовый аналог соответственно, отражающие достижения научно-технического прогресса;
JVi — количество частных научно-технических показателей конкурентоспособности продукции;
Qt, — i.-й обобщённый показатель конкурентоспособности продукции;
— количество частных показателей конкурентоспособности продукции в Ч-м обобщённом показателе;
аи — весовой показатель коэффициента конкурентоспособности продукции;
— количество частных научно-технических показателей конкурентоспособности продукции в ij-м обобщённом показателе;
— количество обобщённых показателей конкурентоспособности продукции;
яр.)
1‘
1 для любого обобщённого показателя
— интегральный показатель конкурентоспособности продукции;
м — количество обобщённых показателей конкурентоспособности продукции в интегральном коэффициенте;
м
Л»”-1 для интегрального показателя
Экономико-математическая модель (8) — (11) позволяет качественно оценить конкурентоспособность продукции с учётом влияния на неё различных производственных и рыночных факторов, распределённых во времени.
Для построения экономико-математической модели распределения инвестиций при модернизации наукоёмких предприятий, нужно ввести ограничения по времени и имеющимся финансовым средствам в модели (8) — (11) и (4) — (7). Данные ограничения важны, потому что любая модернизация конечна и имеет определённый период реализации, в течение которого должны быть достигнуты соответствующие целевые показатели хозяйственной деятельности предприятия.
Так же необходимо конкретизировать понятие потребительского свойства (параметра рассматриваемого товара). В отличие, например, от ноу-хау, потребительское свойство имеет вполне осязаемый характер и поддаётся описанию. А раз так, то можно определить потребительское свойство, как сочетание трёх основных компонентов разработки и производства товаров: трудоёмкости, материалов и оборудования:
Vik = Pik(Lik-Mik,Eik), (12)
iife —
где чк — трудозатраты, выраженные в денежном эквиваленте, на создание (включая распределённые по всему жизненному циклу продукта затраты на разработку данного свойства, НИОКР) i-го потребительского свойства товара к
Mtk — материалы, выраженные в денежном эквиваленте, расходуемые на создание (включая распределённые по всему жизненному циклу продукта затраты на материалы, пошедшие на отработку данного свойства во время проведения НИОКР) i-го потребительского свойства товара к
Еш — производственные затраты машиновремени (оборудования), выраженные в денежном эквиваленте, для создания (включая распределённые по всему жизненному циклу продукта затраты на машиновремя, потраченные на отработку данного свойства во время проведения НИОКР) i-го потребительского свойства товара к.
Соответственно, усовершенствование потребительского свойства Pm связано с определённым изменением затрат, описанных в (12):
Введём определение понятия усовершенствования потребительского свойства:
Усовершенствование потребительского свойства — это такое новое сочетание и ^Еш, при
котором либо затраты на производство данного потребительского свойства будут меньше (удешевление продукции при введении новых технологий) либо данное потребительское свойство перейдёт в другую, более высокую, категорию (переориентир на других потребителей).
Тогда затраты zik в модели (4) — (7) на совершенствование i-го потребительского свойства продукции вида к можно выразить следующим образом:
Чк(Я>т) = ^к ±М1к АЕ11о (1*)
241
Бизнес в законе
3’2021
С учётом ограниченности средств на модернизацию наукоёмких предприятии, получаем, что сумма всех затрат на все изменения не должна превышать некоторую величину ® :
т п т п
Ф = Z = Z Zbii(£ CIS)
fc=it=i fe=ii=i
Если величина Ф задана, то задача модернизации наукоёмких предприятий ставится следующим образом: найти такое оптимальное распределение значе-
ний
aLj^ дМ,
ik u^ik, при котором доход от реализации
производимых товаров F будет максимальным.
Так же нужно помнить, что всякое потребительское свойство имеет свою ценность в определённое время. Ценность потребительского свойства имеет тенденцию к снижению с течением времени. Поэтому при описании нашей экономико-математической модели необходимо учитывать период жизненного цикла продукта T, в течение которого востребованы его потребительские свойства.
Итак, предлагаемая авторами экономикоматематическая модель распределения инвестиций при модернизации наукоёмких предприятий будет выглядеть следующим образом:
где функция ck{.zu-t) определяет цену продукции вида к, на усовершенствование которой было потрачено 2и (к=1,…,т) средств, выделенных на модернизацию, реализуемую в течение жизненного цикла данной продукции.0 a v<zk,n _ ожидаемый объём её
реализации (в натуральных единицах) за время жизненного цикла;
— затраты на усовершенствование потребительских свойств продукции вида к;
пк — число усовершенствуемых потребительских свойств (параметров) продукции вида к;
— трудозатраты, выраженные в денежном эквиваленте, на усовершенствование /-го потребительского свойства товара к;
— материалы, выраженные в денежном эквиваленте, расходуемые на усовершенствование /-го потребительского свойства товара к;
аЕц — производственные затраты машиновремени (оборудования), выраженные в денежном эквиваленте, потраченные на усовершенствование /-го потребительского свойства товара к;
h — перечень потребительских свойств продукции вида k, которые могут быть усовершенствованы в результате выполнения мероприятий по модернизации;
/ — множество видов продукции предприятия, из которых хотя бы одно потребительское свойство можно усовершенствовать в течении времени реализации мероприятий по модернизации;
® — общая сумма инвестиций в модернизацию предприятия;
Qk(Eк) — объём максимально-возможного производства продукции вида к на оборудовании, с величиной модернизации в денежном эквиваленте Ец , т.е. модернизированные производственные мощности;
Тч — жизненный цикл продукта к, в течение которого востребованы его потребительские свойства.
Критерий (16) оптимизационной задачи (16) — (19) определяет максимум дохода от реализации продукции, выпущенной на модернизированных производственных мощностях предприятия.
Сумма (17) характеризует затраты, пошедшие на усовершенствование продукции вида к, путём изменения показателей трудоёмкости, потраченных материалов и используемого оборудования, согласно введённому выше определению понятия усовершенствованного потребительского свойства.
Равенство (18) показывает, что совершенствовать продукцию можно в пределах границ инвестиций, выделенных на модернизацию, и что все выделенные инвестиции идут на модернизацию основного вида деятельности предприятия.
Неравенство (19) представляет собой ограничение на выпуск продукции. Максимальный объём выпускаемой продукции не может превышать имеющиеся производственные мощности предприятия по выпуску данной продукции.
Решением экономико-математической модели (16) -(19) будет вектор распределения инвестиций по трём направлениям: персонал, материалы и оборудование для каждого потребительского свойства каждого типа выпускаемой продукции:
___ ___… _*MuiJ
где &Eik — оптимальные значения вели-
__Щи/
^ik, ^ik
чин^;*:, aMiu, при которых достигается максимум критерия (16).
Таким образом, предложенная экономикоматематическая модель распределения инвестиций при модернизации наукоёмких предприятий позволяет оптимальным образом распределять инвестиции, выделенные на модернизацию предприятия, между тремя основными затратными статьями: трудовыми ресурсами, используемыми при производстве материалами и оборудованием.
Оптимальное распределение инвестиций, полученное в результате решения экономико-математической модели (16) — (19), позволит сэкономить финансовые ресурсы предприятия, поднять квалификацию тех работников, которые действительно нуждаются в повышении квалификации с точки зрения производства продукции, а так же грамотно модернизировать те производственные мощности, которые дадут наибольший вклад в повышение конкурентоспособности и финансовой устойчивости предприятия.
Предложенная экономико-математическая модель в определённой степени является развитием моделей, предложенных в [1 — 3], дополняя их конкретизацией понятия усовершенствования потребительского свойства и вводя ограничения на жизненный цикл продукции. Данная модель может быть детализирована и масштабируема в зависимости от цели модернизации и масштаба предприятия.
Список литературы:
1. Диленко В.А., Шпак С.А. Экономико-математические модели инновационной деятельности производственного предприятия. — Киев, Экономика промышленности, № 1, 2005. — с. 44-53.
2. Савчук А.В. Инновационный уровень промышленной продукции и методы его количественной оценки // Экономика промышленности. Экономика Украины в трансформационный период: Сб. науч. тр. — Донецк: ИЭП НАН Украины, 2001. — с. 72-86.
242
Чурсин А. А., Шмаков Е. В.
ЭКОНОМИКО-МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ИНВЕСТИЦИЙ
3. Чурсин А.А. Теоретические основы управления конкурентоспособностью. Теория и практика. Монография. — М.: Спектр, 2021. — 521 с.
4. Nicholas S. Vonortas / US POLICY TOWARDS RESEARCH JOINT VENTURES — Center for International Science and Technology Policy & Department of Economics The George Washington University, 1999.
Reference list:
1. Dilenko V.A., Shpak S.A. Economic and mathematical models of innovative activity of manufacturing enterprise. — Kiev, Industrial economics, No. 1,2005. — p. 44-53.
2. Savchuk A.V. Innovative level of industrial production and methods of its quantitative assessment // Industrial economics. Economy of Ukraine in the transformation period: Collection of scientific papers. — Donetsk: IIE NAS of Ukraine, 2001. — p. 7286.
3. Chursin A.A. Theoretical basis of competitiveness management. Theory and practice. Monograph. — М.: Spektr, 2021. -521 p.
4. Nicholas S. Vonortas / US POLICY TOWARDS RESEARCH JOINT VENTURES — Center for International Science and Technology Policy & Department of Economics The George Washington University, 1999.
РЕЦЕНЗИЯ
на статью «Экономико-математическая модель оптимального распределения инвестиций при модернизации наукоёмких предприятий» д.э.н. Чурсина Александра Александровича, Шмакова Евгения Вячеславовича Статья посвящена проблеме чрезвычайно актуальной для российских предприятий и организаций. Потребности в их инновационном развитии в настоящее время более чем очевидны, однако ограниченность финансовых средств и их нерациональное использование ведет к замедлению реализации инновационных проектов. Поэтому обращение авторов к вопросам оптимального распределения инвестиций представляется вполне обоснованным, а реализация научного интереса в виде конкретной экономико-математической модели, безусловно, актуальной.
Чурсин А.А. и Шмаков Е.В. рассматривают потребительские свойства товаров, выпускаемых предприятием, через призму значимости их для конечного потребителя. Чем более значимо данное потребительское свойство, тем больше внимание ему нужно уделить при осуществлении модернизационных изменений. При ограниченном финансировании модернизации предприятий точное определение значимых потребительских свойств товара и распределение средств на улучшение в первую очередь именно этих свойств имеет ключевое значение для последующего увеличения прибыли предприятия.
Все отмеченное выше позволяет утверждать, что статья Чурсина А.А. и Шмакова Е.В. «Экономико-математическая модель оптимального распределения инвестиций при модернизации наукоёмких предприятий» представляет несомненную научную и практическую ценность, полностью соответствует всем требованиям, предъявляемым к публикациям в журналах, включенных в перечень ВАК, ранее не публиковалась, и может быть рекомендована к открытой печати в одном из таких журналов.
Заместитель директора по внешнеэкономической деятельности Института прикладных техникоэкономических исследований и экспертиз РУДН, к.э.н.
Т.В. Кокуйцева
243
